Замечания. 1) Для нуль-вектора противоположным будет тоже нуль-вектор

1) Для нуль-вектора противоположным будет тоже нуль-вектор.

2) Вектор противоположный к противоположному к вектору - это вектор ,

то есть -(- ) = .

3) (-1) = - .

4) Для любого вектора существует единственный вектор противоположный к данному.

Теорема. (Правило треугольника для суммы векторов).

Пусть , Î Vⁿ и точки A,B,C Î Eⁿ такие, что 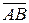= , 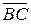= . Тогда = + .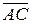

Доказательство.

Пусть = (), = (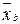), A (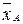), B (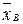) и C (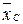), и пусть вектор такой, что

= + .

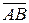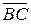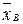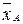Так как = , = , то - = и - = .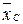

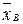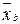Тогда координаты вектора будут следующими:

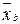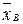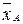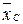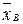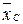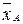+ = ( - ) + ( - ) = - , то есть = .

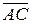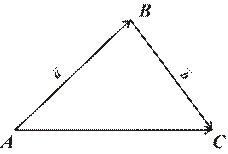
РИС. 21

Следствие. Результат суммы векторов не зависит от выбора системы координат.