Сумма векторов

Пусть в Eⁿ фиксирована декартова система координат.

Определение. Суммой векторов и (, Î Vⁿ) будем называть вектор Î Vⁿ, координаты которого – это сумма координат векторов и , то есть = + .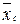

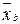Обозначение: = + - «вектор равен сумме векторов и .

Замечание. Определение суммы введено при фиксированной системе координат, и пока не ясно зависит ли результат суммы двух векторов от выбора системы координат.

Теорема. (Свойства суммы векторов).

1. Операция суммы векторов коммутативна, то есть + = + для любых векторов , Î Vⁿ.

2. Операция суммы векторов ассоциативна, то есть + ( + ) = ( + ) + для любых векторов , , Î Vⁿ.

3. Нуль-вектор является нейтральным элементом относительно операции суммы векторов, то есть + q = для любого вектора Î Vⁿ.

4. Для любого вектора Î Vⁿ существует вектор (- )ÎVⁿ такой, что + (- ) = q

5. l ( + ) = l + l для любых векторов , Î Vⁿ и любого числа l Î R.

6. (l + m) = l + m для любого вектора Î Vⁿ и любых чисел l, m Î R.