Доказательство

1) Так как + 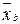= 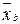+ , то + = + .

2) Так как + ( + 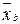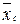) = ( + 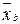) + 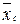, то + ( + ) = ( + ) + .

3) Так как + 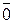= , то + q = .

4) Пусть = (), возьмем вектор (- ) с координатами: (- ) = (- ).

Так как + (- ) = 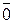, то + (- ) = q.

5) Так как 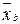l( + ) = l + l 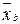, то l( + ) = l + l .

6) Так как (l + m) = l + m , то (l + m) = l + m .

Замечание.

Свойства 1- 4 операции суммы векторов говорят о том, что множество Vⁿ относительно операции суммы – это коммутативная группа.

Определение. Вектор (- ) такой, что + (- ) = q будем называть противоположным к вектору .