Упражнения. 1) Докажите, что | | + | | ³ | + | для любых векторов

1) Докажите, что | | + | | ³ | + | для любых векторов , Î Vⁿ.

2) Докажите правило параллелограмма для суммы векторов, не ссылаясь на правило треугольника.

3) Докажите, что если 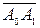= , 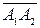= 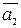, … 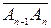= 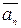(n Î N), то 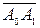+ + 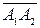…+ 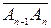= + +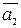…+ 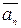(правило многоугольника для суммы векторов).

4) Докажите, что для любого вектора Î Vⁿ существует единственный вектор ÎVⁿ такой, что + = q.

5) Сформулируйте и докажите правило аналогичное правилу треугольника для разности векторов.

§ 11. Базис пространства V².

Теорема (Необходимое и достаточное условие коллинеарности векторов).

Пусть , Î Vⁿ.

Векторы и коллинеарны тогда и только тогда, когда существуют два числа a, b Î R такие, что хотя бы одно из этих чисел не равно нулю* и a + b = q.