Доказательство. 1) Пусть векторы и коллинеарны

1) Пусть векторы и коллинеарны. Докажем, что существуют два числа a, b Î R такие, что хотя бы одно из этих чисел не равно нулю и a + b = q.

1 случай. = q или = q.

Если = q, возьмем a = 1 и b = 0, тогда a + b = 1 ´ q + 0 ´ = q + q = q.

Если = q, то по аналогии возьмем a = 0 и b = 1.

2 случай. ≠ q и ≠ q.

По определению коллинеарности векторов существует число l ≠ 0 такое, что = l .

Возьмем a = l, b = -1, тогда a + b = l + (-1) = + (- ) = q.

2) Пусть a + b = q и из чисел a и b хотя бы одно не равно нулю.

Так как a + b = q, то a = - b .

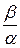
Если a ≠ 0, то = - , и векторы коллинеарны и по определению (см. § 9).
Если a = 0, то b ≠ 0 и вектор = q, то есть векторы и коллинеарны.