Доказательство. 1) Существование чисел x, y

1) Существование чисел x, y.

Возьмем произвольный вектор Î V².

Отложим векторы , и от одной точки O: = , = , = .

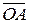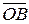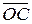Так как векторы и не коллинеарны, то точки O,A,B не лежат на одной прямой.

1 случай. Точка C лежит на прямой OA или на прямой OB.

Если C Î OA, то векторы и коллинеарны и существует такое число l, что = l .

Возьмем x = l и y = 0, тогда x + y = l + 0 = .

Если C Î OB поступим аналогично.

2 случай. Точка C не лежит ни на прямой OA, ни на прямой OB.

Через точку С проведем две прямые: прямую a параллельно прямой OA и прямую b параллельно прямой OB.

Пусть a Ç OB = B’ и b Ç OA = A’.

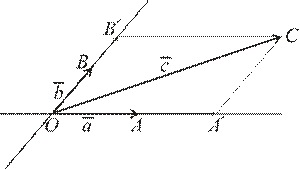
РИС. 23

Четырехугольник OA’CB’ – параллелограмм и ’ + ’ = = .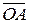

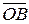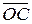Так как точки O,A,A’ лежат на одной прямой, то существует такое число x, что 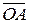’ = x . Аналогично, существует такое число y, что 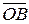’ = y .

Итак, = x + y .

2) Единственность чисел x и y.

Предположим, что для некоторого вектора нашлись два числа x’ и y’ такие, что = x’ + y’ . С другой стороны, существуют два числа x и y, найденные для вектора способом, описанным в пункте 1 и = x + y .

Если = x + y , то - = (-1) (x + y ) = - x - y .

Тогда + (- ) = (x’ + y’ ) + (- x - y ), то есть (x’- x) + (y’- y) = q.

Так как векторы и не коллинеарны, то x’ = x и y’ = y.

Определение. Базисом пространства V² будем называть упорядоченную пару не коллинеарных векторов пространства V².

Определение. Разложить вектор Î V² по базису { , } означает найти два числа x, y Î R такие, что = x + y .

Определение. Координатами вектора в данном базисе будем называть упорядоченный набор коэффициентов в разложении вектора по данному базису, то есть, если = x + y и { , } – базис V², то (x, y) – координаты вектора в базисе { , }.

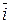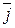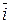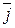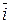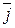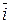Пример. Пусть на плоскости введена декартова система координат. Рассмотрим векторы = (1,0) и = (0,1). Векторы и не коллинеарны (см. § 9), то есть образуют базис пространства V². При этом, для любого вектора Î V² координаты этого вектора в данной системе координат – это и есть его координаты в базисе { , }, то есть « = (x, y) Û = x + y ».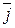

Базис { 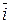, 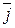} на (евклидовой) плоскости называется стандартным.