2015-04-12
424
1) В треугольнике ABC тока M – середина стороны ВС. Найдите координаты вектора 
= 
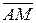в базисе { 
, 
}, где (1) = 
, = 
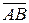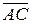; (2) = 
, = 
.
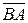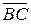2) Точка С делит AB в отношении l. Найдите координаты вектора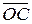 
= в базисе { , }, где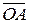 
= , 
= .
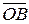3) Пусть векторы , Î V3 не коллинеарны, точки O, A, B Î E3 такие, что 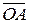= , 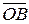= , то есть векторы и отложены от точки O. Докажите, что если для вектора Î V3 существуют два числа x, y Î R такие, что = x + y , и 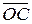= , то точка C лежит в плоскости (OAB). Верно ли обратное?
(Указание. В плоскости (OAB) можно ввести декартову систему координат, как на плоскости E2.)
4) Пусть , Î V2. Докажите, что если для любого вектора Î V2 существуют два числа x, y Î R такие, что = x + y , при этом числа x и у определены однозначно, то векторы и не коллинеарны.
§ 12. Базис пространства V3.
Определение. Векторы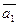 
, 
, …, 
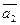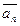Î V3 (n Î N) будем называть компланарными, если существуют их представители (направленные отрезки) с общим началом, которые лежат в одной плоскости.
