1) Ясно, что для любых векторов  ,
,  и
и  можно найти такие три числа a, b, g Î R, что a
можно найти такие три числа a, b, g Î R, что a  + b
+ b  + g
+ g  = q; взять например a = b = g = 0. В теореме утверждается, что для компланарных векторов можно найти числа a, b и g такие, что a ≠ 0 или b ≠ 0 или g ≠ 0.
= q; взять например a = b = g = 0. В теореме утверждается, что для компланарных векторов можно найти числа a, b и g такие, что a ≠ 0 или b ≠ 0 или g ≠ 0.
2) Сформулировать данную теорему можно и иначе (для не компланарных векторов): «Векторы 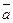 ,
, 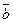 ,
, 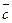 Î V3 – не компланарны тогда, и только тогда, когда равенство a
Î V3 – не компланарны тогда, и только тогда, когда равенство a 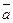 + b
+ b 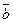 + g
+ g 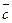 = q возможно только при a = b = g = 0».
= q возможно только при a = b = g = 0».
Теорема.
Пусть 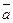 ,
, 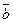 ,
, 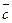 Î V3 – не компланарные векторы. Тогда любого вектора
Î V3 – не компланарные векторы. Тогда любого вектора 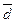 Î V3 существуют три числа x, y, z Î R такие, что
Î V3 существуют три числа x, y, z Î R такие, что 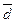 = x
= x 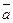 + y
+ y 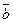 + z
+ z 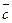 , при этом числа x, y, z определяются однозначно.
, при этом числа x, y, z определяются однозначно.
 2015-04-12
2015-04-12 308
308








