Так как базис пространства - это упорядоченный набор векторов, то при смене порядка векторов базиса получится другой базис. Например, базисы {  ,
,  ,
,  } и {
} и {  ,
,  ,
,  } различны, так как для базиса {
} различны, так как для базиса {  ,
,  ,
,  } первым вектором является вектор
} первым вектором является вектор  , вторым вектором – вектор
, вторым вектором – вектор  , третьим вектором – вектор
, третьим вектором – вектор  , а для базиса {
, а для базиса {  ,
,  ,
,  } первым вектором является вектор
} первым вектором является вектор  , вторым вектором – вектор
, вторым вектором – вектор  , третьим вектором – вектор
, третьим вектором – вектор  .
.
Определение. Разложить вектор 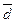 по базису {
по базису { 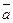 ,
, 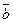 ,
, 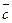 } – это означает представить его в следующем виде:
} – это означает представить его в следующем виде: 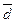 = x
= x 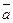 + y
+ y 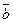 + z
+ z 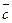 , где x, y, z Î R.
, где x, y, z Î R.
Определение. Координатами вектора в данном базисе будем называть упорядоченный набор коэффициентов в разложении этого вектора по базису.
Пример. В декартовой системе координат рассмотрим векторы 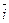 = (1,0,0),
= (1,0,0), 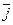 = (0,1,0) и
= (0,1,0) и 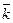 = (0,0,1). Векторы
= (0,0,1). Векторы 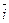 ,
, 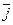 ,
, 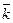 не компланарны (почему?). Координаты вектора
не компланарны (почему?). Координаты вектора 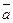 = (x, y, z) в данной системе координат это и есть коэффициенты в разложении вектора
= (x, y, z) в данной системе координат это и есть коэффициенты в разложении вектора 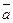 по базису {
по базису { 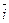 ,
, 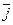 ,
, 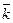 }:
}: 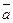 = x
= x 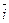 + y
+ y 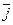 + z
+ z 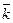 . Базис {
. Базис { 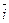 ,
, 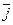 ,
, 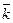 } называют стандартным базисом для евклидова пространства E3 (с фиксированной декартовой системой координат).
} называют стандартным базисом для евклидова пространства E3 (с фиксированной декартовой системой координат).
 2015-04-12
2015-04-12 294
294








