Изменение координат вектора при смене базиса

Vⁿ

Пусть e ₁, e ₂, …, e_n и e ₁’, e ₂’, …, e_n ’ – два базиса пространства Vⁿ.

Для вектора 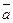определены координаты 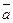в базисе : = , и в базис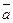е ’: = ’ ’, где

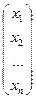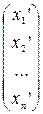= , = (e ₁ e ₂ … e_n), ’= , ’= (e ₁’ e ₂’ … e_n ’)

Для векторов e ₁’, e ₂’, …, e_n ’ определим координаты в базисе e ₁, e ₂, …, e_n:

e ₁’ = a ₁₁ e ₁ + a ₂₁ e ₂ +… a_{n 1} e_n

e ₂’ = a ₂₁ e ₁ + a ₂₂ e ₂ +… a _{2 n} e_n

…

e_n ’ = a_{n 1} e ₁ + a_{n 2} e ₂ +… a_nn e_n, то есть ’ = A, где A = .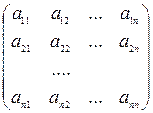

Определение. Матрицу A будем называть матрицей перехода от базиса к базису ’.

Столбцы в матрице перехода от базиса к базису ’ – это координаты векторов e ₁’, e ₂’, …, e_n ’ в базисе .

Итак, = ’ ’= ( A) ’, то есть = (A ’) и = A ’.

Таким образом мы доказали следующую теорему:

Теорема. Пусть и ’ – базисы пространства Vⁿ, A – матрица перехода от базиса к базису ’. Тогда для любого вектора из пространства Vⁿ справедливо равенство = A ’, где – координаты этого вектора в базисе , ’- координаты вектора в базисе ’.