Пусть в En заданы две аффинные системы координат:
«старая» w = (O,  ) и «новая» w’ = (O’,
) и «новая» w’ = (O’,  ’).
’).
Координаты точки M ÎEn
в системе координат w M ( )w, то есть
)w, то есть 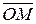 =
= 
 ;
;
в системе координат w’ M ( ’)w’, то есть
’)w’, то есть 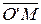 =
=  ’
’  ’.
’.
Координаты точки O’ в системе координат w O’(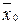 )w, то есть
)w, то есть 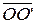 =
= 
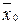 .
.
Пусть A – матрица перехода от базиса  к базису
к базису  ’. Тогда
’. Тогда 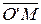 =
=  ’
’  ’=
’=  A
A  ’.
’.
Так как 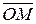 =
= 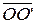 +
+ 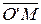 , то
, то 
 =
= 
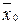 +
+  A
A  ’ =
’ =  (
(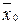 + A
+ A  ’) и,
’) и,
соответственно,  = A
= A  ’ +
’ + 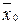
Определение. Матрицу перехода от базиса  к базису
к базису  ’ будем называть матрицей перехода от системы координат w к системе координат w’.
’ будем называть матрицей перехода от системы координат w к системе координат w’.
Итак, мы доказали следующую теорему:
Теорема. Пусть (O,  ) и (O’,
) и (O’,  ’) – аффинные системы координат в En, A – матрица перехода от системы координат w к системе координат w’. Тогда для любой точки из En справедливо равенство
’) – аффинные системы координат в En, A – матрица перехода от системы координат w к системе координат w’. Тогда для любой точки из En справедливо равенство  = A
= A  ’ +
’ + 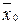 , где
, где  – координаты этой точки в системе координат w,
– координаты этой точки в системе координат w,  ’- координаты этой точки в системе координат w’,
’- координаты этой точки в системе координат w’, 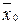 - координаты точки O’ в системе координат w.
- координаты точки O’ в системе координат w.
 2015-04-12
2015-04-12 338
338








