Примеры

1) Рассмотрим две аффинные системы координат w = (O, )

и w’ = (O’, ) (системы координат отличаются лишь выбором начала координат; в таком случае, говорят о параллельном переносе системы координат на вектор ).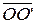

Матрица перехода от w к w’ – это единичная матрица, поэтому формулы преобразования координат будут выглядеть следующим образом:

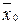= ’+ , где 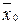- координаты точки O’ в системе координат w.

Тогда ’ = - .

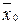Например, уравнение окружности (x – 1)² + (y + 3)² = 1, заданной в декартовой системе координат (O, ), при переходе в новую декартову систему координат с началом в точке O’ (1,-3) и тем же базисом, примет вид: x’² + y’² = 1.

Преобразования координат при этом будут выглядеть следующим образом: .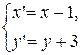

РИС. 27

2) Рассмотрим две декартовы системы координат на плоскости: w = (O, ) и w’ = (O, ’), такие, что их начала координат совпадают, а вектор 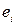составляет с вектором 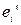угол j (i = 1,2) (см. рис. 28). В таком случае говорят о повороте системы координат вокруг начала на угол j.

РИС. 28

Найдем матрицу перехода от w к w’, для этого вычислим координаты векторов ’ в базисе : 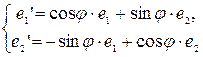, то есть матрица перехода A = .

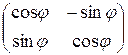Итак, .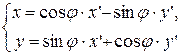

Формулы обратного перехода (от w к w’) можно получить, заменив j на (-j):

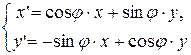, так что B = 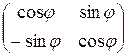- матрица перехода от w’ к w.

Можно проверить, что AB = 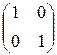= E.