1) Докажите, что если матрица A такая, что det A ≠ 0, то A - это матрица перехода от некоторого базиса к другому базису Vn.
(Указание. Можно рассмотреть отдельно случаи n = 1, 2, 3).
2) Постройте аффинную систему координат (O,  ). На этом же чертеже изобразите систему координат (O’,
). На этом же чертеже изобразите систему координат (O’,  ’), найдите матрицу перехода от базиса
’), найдите матрицу перехода от базиса  к базису
к базису  ’. Определите координаты вектора
’. Определите координаты вектора 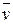 в базисе
в базисе  ’.
’.
| 1. | 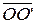 = e1, = e1, 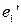 = e1 – e2, = e1 – e2, 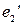 = 2e2; = 2e2; 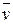 = 3e1 – 2e2; = 3e1 – 2e2;
|
| 2. | В системе координат (O,  ): O’ (1,3), ): O’ (1,3), 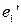 = - e2, = - e2, 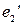 = 2 = 2 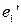 , , 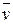 = (-2,1); = (-2,1);
|
 2015-04-12
2015-04-12 225
225








