1. Фокальное свойство: эллипс – это ГМТ (геометрическое место точек), сумма расстояний которых до фокусов постоянна и равна 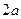 .
.
Доказательство:
Рассмотрим 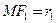 и
и 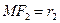 . Покажем, что
. Покажем, что 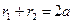 .
.
Найдём 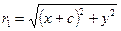 и
и 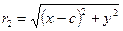 . Тогда
. Тогда 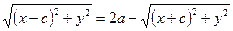 ;
;
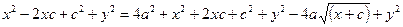 ;
; 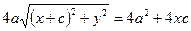 ;
; 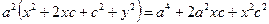 ;
; 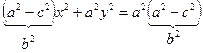 . Разделим обе части равенства на
. Разделим обе части равенства на 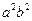 , получим
, получим 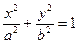 . ■
. ■
2. Директориальное свойства: эллипс – ГМТ (геометрическое место точек), отношение расстояний от которых до фокусов и до соответствующих директрис равно 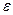 .
.
Доказательство:
Обозначим через 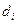 расстояние от точки
расстояние от точки 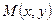 до директрисы
до директрисы 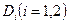 . Покажем, что
. Покажем, что 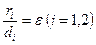 .
.
Пусть 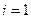 . Тогда
. Тогда 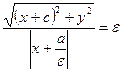 ;
; 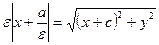 . Так как
. Так как 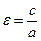 , то
, то 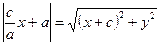 ,
, 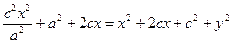 ;
;
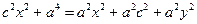 ;
; 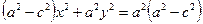
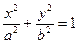 . ■
. ■
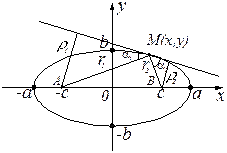 3. Оптическое свойство: эллипс – ГМТ (геометрическое место точек), касательные в которых образуют равные острые углы с фокальными радиусами
3. Оптическое свойство: эллипс – ГМТ (геометрическое место точек), касательные в которых образуют равные острые углы с фокальными радиусами 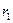 и
и 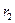 , т.е.
, т.е. 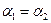 .
.
Другими словами, лучи света, исходящие из одного фокуса 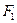 эллипса, после зеркального отражения от эллипса проходят через второй фокус
эллипса, после зеркального отражения от эллипса проходят через второй фокус 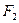 .
.
Касательная в любой точке 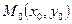 эллипса образует с фокальными радиусами острые одинаковые углы. Это свойство называется оптическим, т.к. все лучи, выходящие из одного фокуса, после отражения оказывается в другом (так как угол падения равен углу отражения).
эллипса образует с фокальными радиусами острые одинаковые углы. Это свойство называется оптическим, т.к. все лучи, выходящие из одного фокуса, после отражения оказывается в другом (так как угол падения равен углу отражения).
Доказательство:
1. Получим сначала уравнение касательной к эллипсу в любой точке 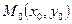 эллипса. Из уравнения эллипса
эллипса. Из уравнения эллипса 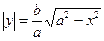 , т.е.
, т.е. 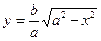 , если
, если 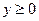 , и
, и 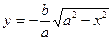 , если
, если 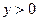 . Тогда и в том и в другом случае
. Тогда и в том и в другом случае 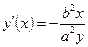 ,
, 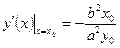 .
.
Таким образом, уравнение касательной к кривой 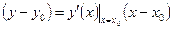 в данном случае имеет вид
в данном случае имеет вид 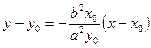 . Умножив это уравнение на
. Умножив это уравнение на 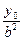 , раскрыв скобки и учтя, что
, раскрыв скобки и учтя, что 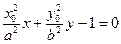 –получим уравнение касательной к эллипсу.
–получим уравнение касательной к эллипсу.
2. Найдём уравнение 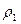 от точки
от точки 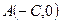 до касательной. Это расстояние
до касательной. Это расстояние 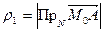 , где
, где 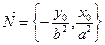 .
.
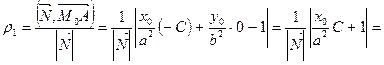
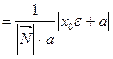 .
.
Но из директориального свойства фокальный радиус 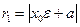 . Таким образом,
. Таким образом, 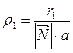 . Тогда
. Тогда  .
.
Проделав аналогичные выкладки, получим, что 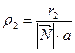 , т.е.
, т.е. 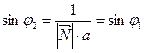 .
.
 2015-06-28
2015-06-28 5347
5347