Из уравнения (1) с помощью элементарных преобразований получим: 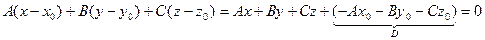 или
или
| (2) | 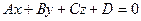 |
– общее уравнение плоскости.
Очевидно, что общее уравнение плоскости является алгебраическим уравнением первого порядка относительно трех переменных 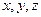 и определяет поверхность первого порядка.
и определяет поверхность первого порядка.
Проведем исследование (положение плоскости в частных случаях).
А) 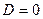 ,
, 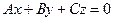 .
.
Т.к. координаты точки 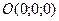 - удовлетворяют данному уравнению, плоскость проходит через начало координат.
- удовлетворяют данному уравнению, плоскость проходит через начало координат.
Б) 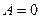 ,
, 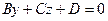 ,
, 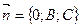 , значит
, значит 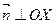 , следовательно
, следовательно 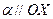 .
.
Аналогично, если 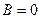 ,
, 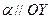 ;
; 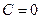 ,
, 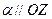 .
.
В) При 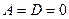 ,
, 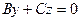 . Плоскость проходит через ось
. Плоскость проходит через ось 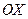 .
.
Аналогично, при 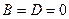 – плоскость проходит через ось
– плоскость проходит через ось 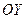 ;
;
при 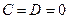 – плоскость проходит через ось
– плоскость проходит через ось 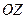 .
.
Г) 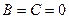 ,
, 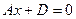
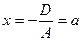 . Данное уравнение определяет плоскость, параллельную
. Данное уравнение определяет плоскость, параллельную 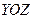 , т.к.
, т.к. 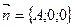 ,
, 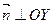 ,
, 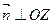 .
.
Аналогично, 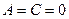
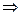
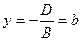 ,
, 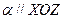 ;
; 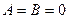
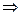
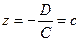 ,
, 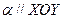 .
.
Д) 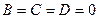 ,
, 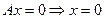 (
(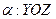 ).
).
Аналогично, 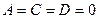 ,
, 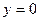 (
(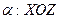 );
); 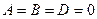 ,
, 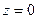 (
(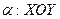 ).
).
 2015-04-12
2015-04-12 1122
1122
