Взаимное расположение плоскостей в пространстве

Пусть 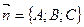- нормальный вектор для плоскости .

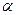Утверждение 1. Вектор 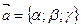параллелен плоскости 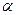, заданный уравнением (14.2) тогда и только тогда, когда

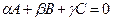. (6)

Утверждение 2. Плоскость 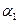, заданная уравнением 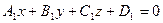и плоскость 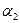, заданная уравнением 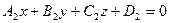параллельны тогда и только тогда, когда

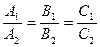. (7)

Доказательство. Действительно, 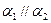, есл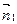и и 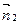коллинеарны, т.е. 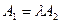, , 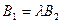, 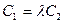т.е. 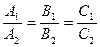. Верно и обратное.

Утверждение 3. Плоскост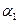и и 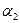совпадают тогда и только тогда, когда

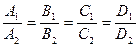. (8)

Утверждение 4. Плоскост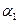и и 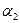пересекаются тогда и только тогда, когда 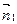и 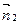неколлинеарны, причем угол между ними равен углу между нормальными векторами.

Утверждение 5. Пусть плоскост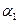и и 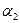пересекаются по прямой, тогда плоскость 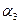проходит через эту прямую, причем ее уравнение имеет вид:

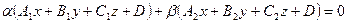, где 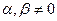одновременно. (14.9)