2015-04-12
404
Для того чтобы однозначно определить положение плоскости в пространстве достаточно задать одну точку М 0(x 0; у 0; z 0) на плоскости и нормальный вектор N = { A; B; C }, перпендикулярный к этой плоскости, или задать три точки на плоскости.
Построим уравнение плоскости при произвольных М 0 и N.
1) Пусть M (x; y; z) – произвольная точка плоскости.
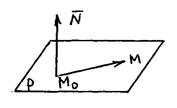2) Общее свойство: любой вектор, лежащий на плоскости, в том числе 
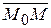= { x – x 0; y – y 0; z – z 0}, перпендикулярен нормальному вектору N,т.е. 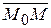N = 0.
3) В координатной форме это условие перпендикулярности приводит к уравнению плоскости, заданной точкой и нормальным вектором
A (x – x 0) + B (y – y 0) + C (z – z 0) = 0. (15)
Общее уравнение плоскости имеет вид:
Ax + By + Cz + D = 0, (16)
где коэффициенты A, B, C являются координатами нормального вектора плоскости N и D = –(Ax 0 + By 0 + Cz 0).
Частные случаи общего уравнения плоскости:
1) при А = 0 плоскость By + Cz + D = 0 параллельна оси Ох;
2) при B = 0 плоскость Ax + Cz + D = 0 параллельна оси Оy;
3) при А = B = 0 плоскость Cz + D = 0 параллельна плоскости хОу и т.д.
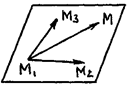
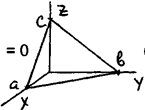Даны три точки М 1(x 1; у 1; z 1), М 2(x 2; у 2; z 2), М 3(x 3; у 3; z 3). Построим уравнение плоскости p, проходящей через эти точки.
|
|
|
1) Пусть M (x; y; z) – произвольная точка плоскости.
2) Общее свойство: любые вектора, лежащий в плоскости, в том числе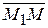 
= { x – x 1; y – y 1; z – z 1}, 
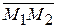= { x 2 – x 1; y 2 – y 1; z 2 – z 1}, 
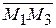= { x 3 – x 1;
y 3 – y 1; z 3 – z 1}, коллинеарны.
3) Условие коллинеарности трех векторов – их смешанное произведение равно нулю, и дает уравнение плоскости по трем заданным точкам
= 
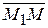
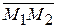
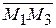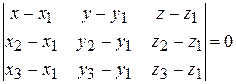. (17)
Если в качестве трех точек взять точки пересечения плоскости с осями координат (a; 0; 0), (0; b; 0), (0; 0; c), то получим уравнение плоскости в отрезках
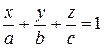. (18)
