Прямая и плоскость

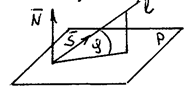
Угол между прямой и плоскостью. Углом 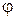между прямой l и плоскостью p называется любой из двух смежных углов образованных между l и ее проекцией на плоскость p.

Дано S = { m; n; p }, N = { A; B; C }, тогда

sin 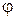= |cos(N ^ S)| = 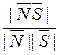. (30)

Если l 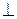p, то

S || N 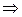S ´ N = 0 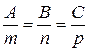. (31)

Если l || p, то

S 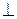N SN = 0 Am + Bn + Cp = 0. (32)

Пример. Вычислить точку пересечения прямой 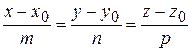с плоскостью Ax + By + Cz + D = 0.

Решение. Уравнения прямой представим в параметрическом виде

x = x ₀ + 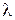m, y = y ₀ + 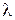n, z = z ₀ + 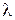p. (33)

Точка пересечения имеет конкретное значение параметра 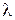_п и удовлетворяет уравнению плоскости. Подставим координаты (33) в уравнении плоскости

A (x ₀ + l m) + B (y ₀ + l n) + C (z ₀ + l p) + D = 0.

Решение этого уравнения относительно l и определит параметр точки пересечения l и p

.

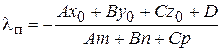Уравнения (33) при l = l_п определят координаты точки пересечения прямой и плоскости.

Решение типичных задач

Пример 5. Найти уравнение плоскости p, проходящей через точку
М (2; 2; –3) и параллельной плоскости p ₁: х – 4 у – 2 z + 1 = 0 N ₁ = {1; –4; –2}.

Решение. Из условия p ₁ || p N ₁ || N. Пусть N = N ₁ = {1; –4; –2}, тогда имеем точку М ₀, вектор N и уравнение плоскости A (x – x ₀) + B (y – y ₀) +
+ C (z – z ₀) = 0, т.е. p: 1(x – 2) – 4(y – 2) – 2(z + 3) = 0 х – 4 у – 2 z = 0.

Пример 6. Найти уравнение плоскости p, проходящей через точку
М ₀(–1; 2; 3) и через ось Oz.

Решение. Т.к. p проходит через Oz и начало координат, то в уравнении Ax + By + Cz + D = 0, где D = –(Ax ₀ + By ₀ + Cz ₀), имеем C = 0 и D = 0. Тогда из условия D = A – 2 B = 0 A = 2 B и p: 2 Bx + By = 0 или 2 x + y = 0.

Пример 7. Найти уравнение плоскости, проходящей через точки
М ₁(0; 2; 3), М ₂(–1; 0; 1), М ₃(2; 1; –1).

Решение. Введем вектора 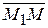= { x; y – 2; z – 3}, 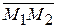= {–1; –2; –2}, 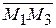= {2; –1; –4} и вычислим их смешанное произведение

= =

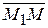
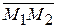
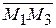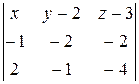= х 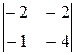– (у – 2) 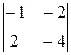+ (z – 3) 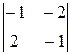= 6 x – 8 y + 5 z + 1 = 0

N = {6; –8; 5}.

Пример 8. При каких А и С плоскости p ₁: Ax + 2 y – z + 3 = 0
N ₁ = { A; 2; –3} и p ₂: 2 x + 6 y – Cz + 7 = 0 N ₂ = {2; 6; – C } параллельны?

Решение. Из условия p ₁ || p ₂ N ₁ || N ₂, т.е. координаты векторов пропорциональны: 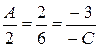А = 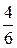= 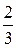, С = 9.

Пример 9. Найти расстояние между параллельными плоскостями
p ₁: 6 х + 2 у + 9 z = 0 N ₁ = {6; 2; 9} и p ₂: 6 x + 2 y + 9 z – 11 = 0 N ₂ = {6; 2; 9}.

Решение. На p ₂ выберем точку М ₀. Пусть x = y = 0, тогда z = 11/9, т.е. М ₀(0; 0; 11/9). Расстояние от М ₀(x ₀; у ₀; z ₀) до плоскости Ax + By + Cz + D = 0 определяет формула d = | Ax ₀ + By ₀ + Cz ₀ + D | / | N |, т.е. d = .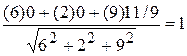

Пример 10. Перейти от общего уравнения прямой 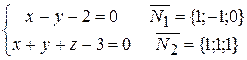к каноническому уравнению.

Решение: Координаты N ₁ и N ₂ не пропорциональны, т.е. векторы не коллинеарны, плоскости пересекаются, линия пересечения имеется. Направляющий вектор S = N ₁ ´ N ₂ = 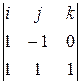= – i – j + 2 k = {–1; –1; 2}. Пусть в системе уравнений z = 0, тогда система упростится: 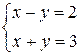и даст решение: х = 2,5; у = 0,5. В результате имеем S = {–1; –1; 2}, M ₀(2,5; 0,5; 0) и каноническое уравнение (24) примет вид .

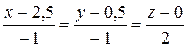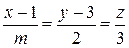
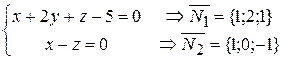Пример 11. При каком m прямые l ₁: S ₁ = { m; 2; 3}, M ₀(1; 3; 0) и l ₂: перпендикулярны?

Решение. Определим S ₂ = N ₁ ´ N ₂ = 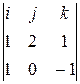= –2 i + 2 j – 2 k.

Из условия l ₁ 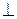l ₂ S ₁ S ₂ = 0 или m (–2) +2(2) + 3(–2) = 0 m = –1.

Пример 12. Найти параметрические уравнения прямой l, проходящей через точку М ₀(–1; 2; 3) и перпендикулярной к плоскости p: 3 x + y – 5 z + 1 = 0 N = {3; 1; –5}.

Решение. Если l 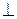p, то N || S. Пусть S = { m; n; p } = N = {3; 1; –5}, тогда параметрические уравнения x – x ₀ = 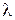m, y – y ₀ = 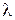n, z – z ₀ = 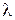p принимают вид: х + 1 = 3 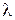, y – 2 = 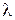, z – 3 = –5 .

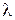Пример 13. Найти точку пересечения плоскости x – 2 y + 3 z + 5 = 0 N = {1; –2; 3} и прямой 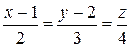S = {2; 3; 4}, M ₀(1; 2; 0).

Решение: параметрические уравнения прямой: x = 2l + 1, y = 3l + 2,
z = 4l подставим в уравнение плоскости (2l + 1) – 2(3l + 2) + 3(4l) + 5 = 0 и получим l_п = –1/4. Заменив в параметрических уравнениях параметр l на –1/4 находим координаты точки пересечения прямой и плоскости (0,5; 5/4; –1).

Пример 14. Найти угол между прямой l: 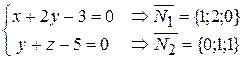и плоскостью p: 2 x + y – z + 1 = 0 N = {2; 1; –1}.

Решение. Направляющий вектор l: S = N ₁ ´ N ₂ = 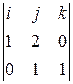= 2 i – j + k.

Угол между l и p: sin 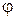= |cos(N ^ S)| = | NS | / | N || S |, т.е.

sin = = .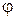

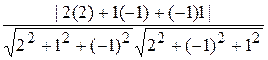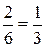Задачи для самостоятельного решения

11) Найти уравнение плоскости, проходящей через две данные прямые , .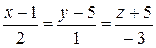

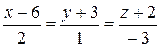12) Найти каноническое уравнение прямой, проходящей через точку М (3; 1; 5) перпендикулярно плоскости, проходящей через точки А (1; 2; 0), В (4; 2; 2), С (0; 1; 2).

13) Найти расстояние от точки М (–1; 3; 5) до плоскости, проходящей через точку А (2;–2; 1) перпендикулярно прямой .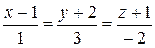

14) Найти уравнения плоскости, проходящей через точки А (0; 3; 3),
В (3; 1; –5) и параллельной оси Ох.

15) Найти расстояние от точки А (1; –2; 3) до плоскости, проходящей через точку М (–1; 2; 3) и ось Оу.

16) Найти каноническое уравнение прямой, проходящей через точку М (0; 1; 2) параллельно прямой .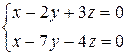

17) Найти каноническое уравнение прямой, проходящей через точку М (1; 2; 3) перпендикулярно прямой .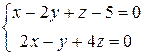

18) Найти угол между прямыми , .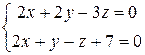

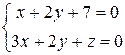19) Найти уравнение плоскости, проходящей через точку А (5; 4; 2) и содержащей прямую .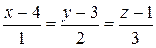

20) Найти угол между плоскостью х + 2 у – z + 2 = 0 и плоскостью, проходящей через точки А (2; –2; –3), В (3; 0; –5), С (5; –2; 0).