2015-04-12
703
Каноническое уравнение прямой. Заданы точка М 0(x 0; у 0; z 0) на прямой и ее направляющий вектор S = { m; n; p }.
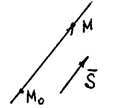1) Пусть М (x; y; z) – произвольная точка линии.
2) Общее свойство: любой отрезок прямой, в том числе вектор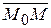 
, коллинеарен вектору S, т.е. = 
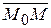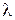S.
3) В координатной форме это условие дает три равенства
x – x 0 = 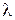m; y – y 0 = 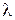n; z – z 0 = 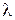p, (20)
которые называются параметрическим уравнением прямой. Исключим параметр 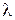в (20) и получим систему из двух канонических уравнений прямой в пространстве
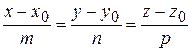. (21)
Уравнение прямой, проходящей через две заданные точки М 1(x 1; у 1; z 1), М 2(x 2; у 2; z 2). Вектор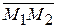 
= { x 2 – x 1; y 2 – y 1; z 2 – z 1} = S в данном случае является направляющим и уравнения (21) принимают вид
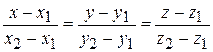. (22)
Общее уравнение прямой. Прямую в пространстве можно определять также как линию пересечения двух не параллельных плоскостей
A 1 x + B 1 y + C 1 z + D 1 = 0, N 1 = { A 1; B 1; C 1},
A 2 x + B 2 y + C 2 z + D 2 = 0, N 2 = { A 2; B 2; C 2}. (23)
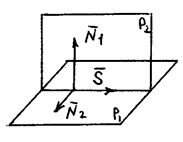Линия пересечения l перпендикулярна векторам N 1 и N 2. Векторное произведение N 1 ´ N 2 также перпендикулярно N 1, N 2 (по определению) и поэтому его можно взять в качестве направляющего вектора S линии l
|
|
|
S = N 1 ´ N 2 =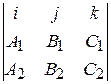 
= { m; n; p }. (24)
Для полного перехода от общего уравнения прямой (23) к каноническому уравнению (21) достаточно дополнительно найти координаты некоторой точки линии – М 0(x 0; у 0; z 0). Для этого в уравнениях (23) одну из координат приравняем к нулю, а остальные вычислим, решив систему двух уравнений для двух неизвестных.
Пример. Перейти от общего уравнения прямой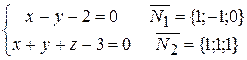 
к каноническому уравнению.
Решение. Координаты N 1 и N 2 не пропорциональны, т.е. векторы не коллинеарны, плоскости пересекаются, линия пересечения имеется.
S =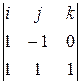 
= – i – j + 2 k = {–1; –1; 2}. Пусть в системе уравнений
z = 0, тогда система упростится: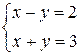 
и даст решение: х = 2,5, у = 0,5.
В результате имеем S = {–1; –1; 2}, M0(2,5; 0,5; 0) и каноническое уравнение (21) примет вид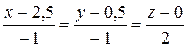 
.
Угол между двумя плоскостями p 1 и p 2 (23) равен углу между их нормальными векторами N 1, N 2
= 
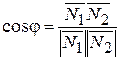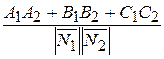. (25)
Если плоскости параллельны: p 1 || p 2, то и N 1 || N 2 
N 1 ´ N 2 = 0, т.е. соответствующие координаты нормальных векторов пропорциональны
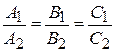. (26)
Если плоскости перпендикулярны: p 1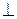 
p 2, то и N 1 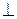N 2 N 1 N 2 = 0 или
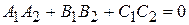. (27)
