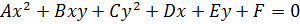Кривые второго порядка. Окружность

(1) – общее уравнение второй степени относительно x и y. A, B, C, D, E, F 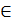R; A, B, C одновременно 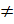0
Опр. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат.
Кривыми второго порядка являются: эллипс (частный случай – окружность); гипербола; парабола.

Опр. Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром.

Рассмотрим на плоскости Oxy (в прямоугольной декартовой системе координат) окружность радиуса R с центром в т. C(a; b) и составим её уравнение

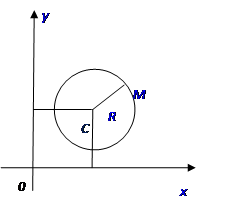
C(a; b) – центр окружности

M(x; y) – произвольная точка окружности

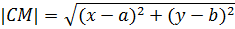
По определению 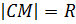, значит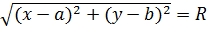
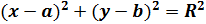(2) – уравнение окружности с центром в т. C(a; b) и радиусом R.

Частный случай: 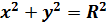– уравнение окружности с центром в т. O(0;0) и радиусом R.

Раскроем скобки в уравнении (2)

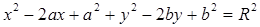
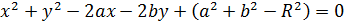
Обозначим ; ; .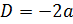

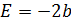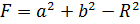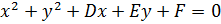– уравнение второй степени относительно x и y.
Его особенности: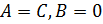

Обратно, если в (1) 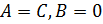, то (1) определяет окружность.

Пример 2.1. Дано уравнение 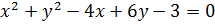. Доказать, что это уравнение определяет окружность. Найти центр и радиус.