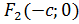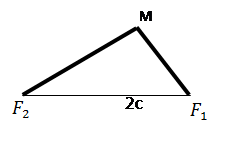 Опр. Эллипсом называется геометрическое место точек, сумма расстояния которых до двух данных точек, называемых фокусами, есть величина постоянная.
Опр. Эллипсом называется геометрическое место точек, сумма расстояния которых до двух данных точек, называемых фокусами, есть величина постоянная.
|
|
|
Обозначим 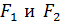 – фокусы,
– фокусы,
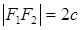 – расстояние между фокусами.
– расстояние между фокусами.
М – производная точка эллипса.
2а – постоянная величина, равная сумме расстояний от М до 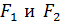
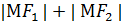 =const=2 a (1) – определение эллипса
=const=2 a (1) – определение эллипса
2a>2c 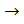 a>c (две стороны больше одной)
a>c (две стороны больше одной)
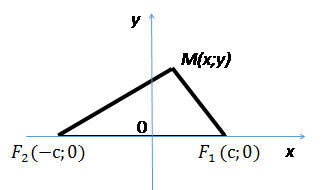 Введем систему координат следующим образом: ось OX проведем через фокусы
Введем систему координат следующим образом: ось OX проведем через фокусы 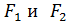 , начало координат поместим в середину отрезка
, начало координат поместим в середину отрезка 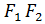 . Ось OY через середину
. Ось OY через середину 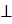 OX.
OX.
М (x; y) – произведения точка эллипса
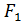 (c;0),
(c;0), 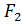 (– c;0) – фокусы эллипса
(– c;0) – фокусы эллипса
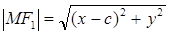
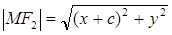
Подставим в (1), получим 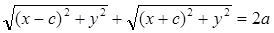 (2) – уравнение эллипса в выбранной системе координат.
(2) – уравнение эллипса в выбранной системе координат.
Упростим данное уравнение:
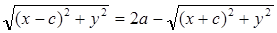
Возведем обе части в квадрат:
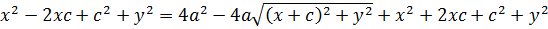
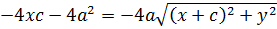
Разделим на (-4): 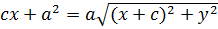
Возведем в квадрат:
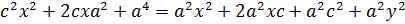
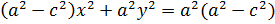
Разделим на 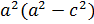 :
: 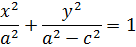
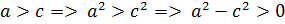 Обозначим:
Обозначим: 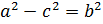
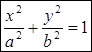 (3) – каноническое уравнение эллипса, где
(3) – каноническое уравнение эллипса, где 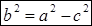
 2015-04-12
2015-04-12 1400
1400

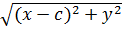 +
+