Геометрический смысл смешанного произведения. Теорема 2.Смешанное произведение равно объему параллелепипеда, построенному на приведённых к общему началу векторах

Теорема 2. Смешанное произведение 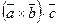равно объему параллелепипеда, построенному на приведённых к общему началу векторах, взятому со знаком <+>, если 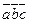– правая тройка векторов, и со знаком <->, если тройка 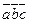– левая.

Если векторы 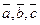– компланарны, то объем равен нулю, и .

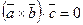Доказательство. Пусть S – площадь параллелограмма, построенного на векторах 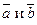, 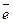– единичный вектор, перпендикулярный к векторам 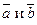и образующий с ними правую тройку. (Вектор 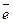– орт векторного произведения .)

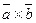Из геометрического свойства 2 векторного произведения

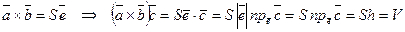(18)

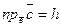– высота параллелепипеда, построенного на векторах 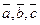, с основанием S.

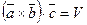, а 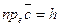, если 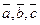правая тройка, то есть той же ориентации, что и .

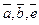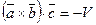, а 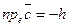, если тройка 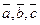левая.

Если векторы 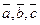– компланарны, то .

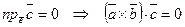Следствие 1. .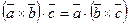

Доказательство. Скалярное произведение векторов коммутативно, следовательно

.

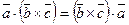По теореме 2: , .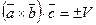

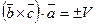Далее будем обозначать смешанное произведение 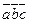, так как .

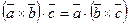Следствие 2. Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны.