Теорема 1. Пусть векторы 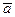 и
и 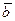 имеют координаты
имеют координаты
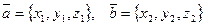 .
.
Векторное произведение этих векторов имеет координаты
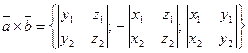 . (16)
. (16)
Можно расписать определители:
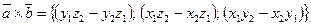 (16’)
(16’)
или представить в виде
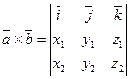 . (16’’)
. (16’’)
Доказательство. Рассмотрим векторные произведения базисных векторов:
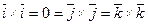
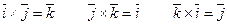 (17)
(17)
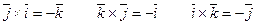 .
.
Разложим векторы 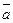 и
и 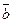 по базису
по базису 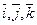 :
:

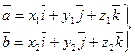 .
.
На основании свойств векторного произведения мы можем перемножать правые части почленно:
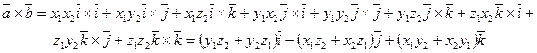
с учетом формул (17).
Пример 1. Найти координаты векторного произведения векторов
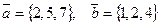 .
.
Решение. Пусть 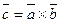 .
.
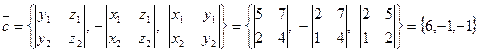 .
.
Пример 2: Даны три точки: 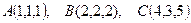 .
.
Найти площадь треугольника АВС (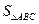 ).
).
Решение.
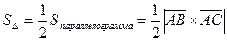 .
.
Найдем координаты векторов 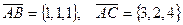 .
.
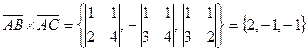 .
.
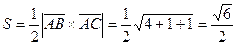 .
.
 2015-04-12
2015-04-12 593
593








