2015-04-12
3262
Задача 1. Разложить вектор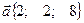 
по векторам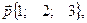 
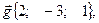
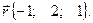
Решение. Разложить вектор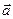 
по векторам 
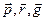– значит представить его в виде
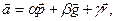(1)
где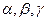 
- неизвестные пока числа. Переходя в равенстве (1) к координатам векторов, получим
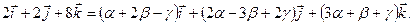
Как известно у равных векторов равны соответствующие координаты,
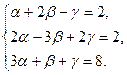(2)
Решив систему (2), найдём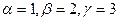 
. Следовательно, 
.
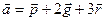Задача 2. Найти вектор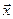 
коллинеарный вектору 
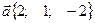и удовлетворяющий условию 
.
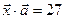Решение. В силу коллинеарности векторов 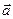и 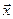вектор 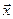можно представить в ви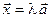де 
где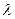 
– пока неизвестный множитель. Для его определения используем второе условие:
.
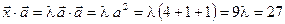Отсюда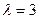 
, поэтому 
.
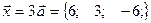Задача 3. Найти вектор 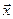, перпендикулярный векторам 
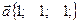и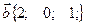 
и образующий с осью Ох тупой угол, если 
.
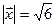Решение. Найдём вектор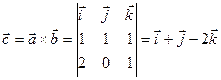 
.
Так как 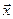перпендикулярен векторам 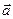и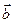 
, то он коллинеарен вектору 
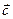. Следовательно, 
.
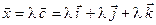По условию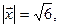 
т.е. 
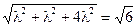или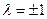 
. Вектор 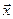образует тупой угол с осью Ох, поэтому его проекция на эту ось должна быть отрицательной, отсюда 
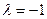и 
.
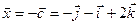Поверхности в пространстве. 2
Плоскость. 2
Неполные уравнения плоскости. 4
Уравнение плоскости в «отрезках». 4
|
|
|
Угол между плоскостями. 5
Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой. 6
Нормальное уравнение плоскости. Расстояние от точки до плоскости. 7
Расстояние от точки до плоскости. 8
Приведение общего уравнения плоскости к нормальному виду. 9
Примеры задач на тему «Плоскость». 9
Поверхности в пространстве
Пусть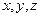 
– переменные.
Выражение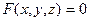 
называется уравнением, если оно выполняется не для любых значений .
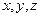Уравнению поверхности удовлетворяют только точки поверхности и никакие другие точки пространства.
Определение. Поверхность – это геометрическое место точек, координаты которых удовлетворяют данному уравнению .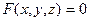
Пример: 
уравнение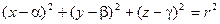 
задает сферу с центром в точке (
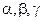), радиусом 
.
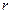Алгебраические поверхности определяются в декартовой системе координат алгебраическими уравнениями вида:
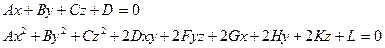
Уравнение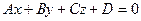 
– общее уравнение первой степени.
