Теорема 3. Пусть векторы 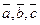 имеют в ортонормированном базисе координаты
имеют в ортонормированном базисе координаты 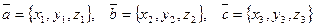 . Тогда смешанное произведение этих векторов можно представить в виде
. Тогда смешанное произведение этих векторов можно представить в виде
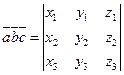 .
.
Доказательство. 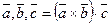 .
.
По теореме о векторном произведении:
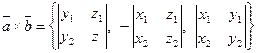 .
.
Умножим векторное произведение скалярно на вектор 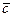 :
:
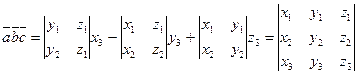 .
.
По следствию 2 необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, составленного из координат векторов:
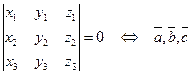 компланарны.
компланарны.
Пример 3. Даны четыре точки: 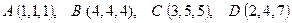 . Найти объем тетраэдра АВСD.
. Найти объем тетраэдра АВСD.
Решение. Объем тетраэдра равен одной шестой объема параллелепипеда с теми же основанием и высотой:
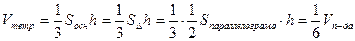 .
.
По теореме 3
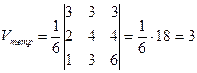 .
.
 2015-04-12
2015-04-12 1175
1175

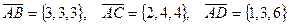 .
.






