3. Антикоммутативность: 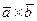 =
= 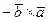
Доказательство. Модули векторов 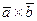 и
и 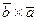 равны по определению векторного произведения. Проверим их направление:
равны по определению векторного произведения. Проверим их направление:
а) 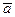 ||
|| 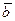
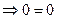 равенство выполняется;
равенство выполняется;
б) 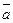 и
и 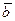 не параллельны. Но
не параллельны. Но 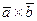 ||
|| 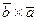 по определению векторного произведения, тогда либо
по определению векторного произведения, тогда либо 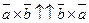 , либо
, либо 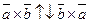 . Пусть
. Пусть 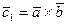 , а
, а 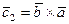 . Тройка векторов
. Тройка векторов 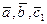 правая, а тройка
правая, а тройка 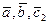 – левая. Следовательно,
– левая. Следовательно, 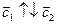 и
и 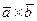 =
= 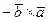 .
.
4. Ассоциативность относительно умножения на число.
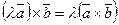
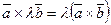
проверяем модуль:
а) 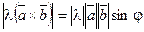 ,
, 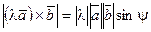 ,
,
где 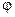 – угол между векторами
– угол между векторами 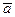 и
и 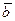 , а
, а 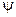 – угол между векторами
– угол между векторами 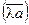 и
и 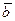 .
.
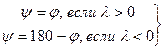 =>
=> 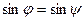
поверяем направление:
б) если 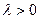
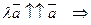
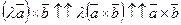
если 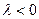
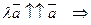
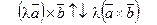 и
и 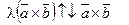
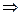
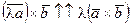 .
.
5. Дистрибутивность относительно сложения векторов
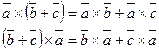
 2015-04-12
2015-04-12 1026
1026








