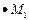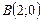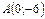Пример 1. Построить прямые:
а) 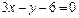 ; б)
; б) 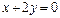 ; в)
; в) 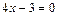 ; г)
; г) 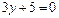 .
.
Решение.
а) Для построения прямой достаточно знать координаты двух ее произвольных точек. Полагая в уравнении 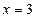 , получим
, получим 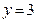 . Точка
. Точка 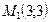 лежит на прямой. Полагая
лежит на прямой. Полагая 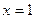 , получим
, получим 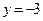 . Вторая точка
. Вторая точка 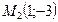 . Проводим прямую
. Проводим прямую 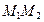 (рис. 4.1).
(рис. 4.1).
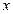
Рис. 4.1 | Задачу можно решить иначе, используя уравнение прямой в отрезках. Приведем уравнение к виду (4.5). Для этого перенесем свободный член (-6) в правую часть уравнения и обе его части разделим на 6. Получим: 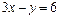 ; ; 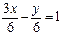 ; ; 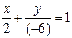 . На оси . На оси 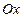 отложим 2 единицы вправо от точки отложим 2 единицы вправо от точки 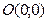 . На оси . На оси 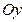 отложим 6 единиц вниз. отложим 6 единиц вниз. |
Получим точки 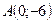 и
и 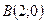 на осях, через которые проведем прямую.
на осях, через которые проведем прямую.
б) Прямая 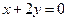 проходит через точку
проходит через точку 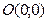 .
.
 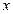 Рис. 4.2 | Полагая 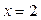 , получаем , получаем 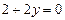 , , 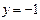 . Точка . Точка 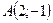 лежит на прямой. Проводим прямую через точки лежит на прямой. Проводим прямую через точки 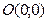 и и 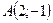 (рис. 4.2). (рис. 4.2). |
в) Разрешим уравнение относительно 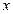 , получаем
, получаем 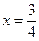 . Это прямая, параллельная оси
. Это прямая, параллельная оси 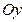 , отсекает на оси
, отсекает на оси 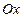 отрезок, равный
отрезок, равный 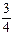 .
.
г) Запишем уравнение в виде 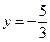 . Эта прямая параллельна оси
. Эта прямая параллельна оси 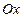 .
.
Пример 2. Уравнение прямой 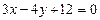 представить в различных видах (с угловым коэффициентом, в отрезках).
представить в различных видах (с угловым коэффициентом, в отрезках).
Решение. Для получения уравнения прямой с угловым коэффициентом разрешим заданное уравнение относительно 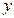 . Получим
. Получим 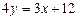 ,
, 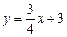 - уравнение прямой с угловым коэффициентом: здесь
- уравнение прямой с угловым коэффициентом: здесь 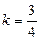 ;
; 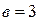 .
.
Для получения уравнения в отрезках на осях координат перенесем свободный член 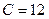 в правую часть и разделим обе части уравнения на (-12). Получим
в правую часть и разделим обе части уравнения на (-12). Получим 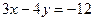 ,
, 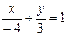 - уравнение в отрезках: здесь
- уравнение в отрезках: здесь 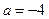 ;
; 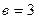 .
.
Пример 3. Составить уравнение прямой, проходящей через точку 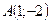
а) под углом 1350 к оси 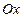 ;
;
б) параллельно оси 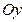 ;
;
в) перпендикулярно вектору 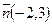 ;
;
г) и точку 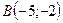 .
.
 2015-04-12
2015-04-12 1228
1228