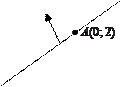а) Уравнение стороны 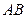 данного треугольника найдем с использованием формулы (4.3):
данного треугольника найдем с использованием формулы (4.3): 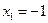 ,
, 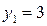 ;
; 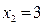 ,
, 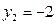 :
: 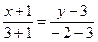 ;
; 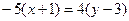 ;
;
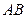 :
: 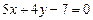 .
.
б) Чтобы составить уравнение медианы 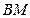 , найдем координаты точки
, найдем координаты точки 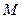 - середины отрезка
- середины отрезка 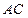 :
:
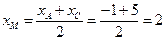 ,
, 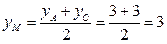 ,
,
т.е. 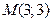 .
.
По формуле (4.3) 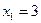 ,
, 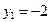 ;
; 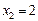 ,
, 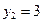 , имеем
, имеем
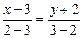 ;
; 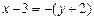 ;
;
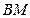 :
: 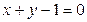 .
.
в) Высота 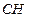 из вершины
из вершины 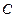 есть прямая, перпендикулярная
есть прямая, перпендикулярная 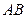 и проходящая через точку
и проходящая через точку 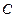 . Вектор
. Вектор 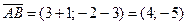 является нормальным вектором высоты. Воспользуемся уравнением (1.2):
является нормальным вектором высоты. Воспользуемся уравнением (1.2):
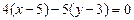 ;
; 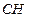 :
: 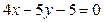 .
.
Угол между медианой 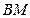 и высотой
и высотой 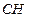 найдем по формуле (1.7). Угловой коэффициент медианы из уравнения медианы:
найдем по формуле (1.7). Угловой коэффициент медианы из уравнения медианы:
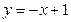 ;
; 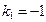 .
.
Угловой коэффициент высоты 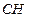 из уравнения
из уравнения 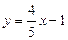 равен
равен 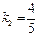 :
: 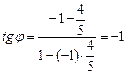 ;
; 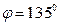 .
.
Пример 6. Построить множество решений неравенства 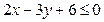 .
.
Решение. Множество решений линейного неравенства с двумя переменными 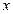 и
и 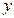 является одна из полуплоскостей, на которые делится вся плоскость прямой
является одна из полуплоскостей, на которые делится вся плоскость прямой 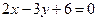 .
.

Рис. 4.3 | Полагая 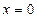 , получим , получим 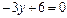 , , 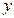 =2. Полагая =2. Полагая 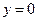 , получим , получим 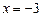 . . 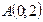 , , 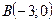 - это точки пересечения прямой с осями координат. Построим прямую (рис. 4.3). Для определения искомой полуплоскости рекомендуется задать произвольную контрольную точку, не лежащую на ее границе – построенной прямой. - это точки пересечения прямой с осями координат. Построим прямую (рис. 4.3). Для определения искомой полуплоскости рекомендуется задать произвольную контрольную точку, не лежащую на ее границе – построенной прямой. |
Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости.
|
|
|
И, наоборот, в случае невыполнения неравенства в контрольной точке, оно не выполняется во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости.
В качестве контрольной точки удобно взять начало координат 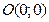 , не лежащей на построенной прямой. Координаты точки
, не лежащей на построенной прямой. Координаты точки 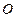 не удовлетворяют неравенству
не удовлетворяют неравенству 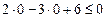 , следовательно, решением данного неравенства является верхняя полуплоскость, не содержащая контрольную точку
, следовательно, решением данного неравенства является верхняя полуплоскость, не содержащая контрольную точку 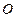 (рис. 4.3).
(рис. 4.3).
 2015-04-12
2015-04-12 1013
1013