Доказательство

Пусть у треугольников ABC и A1B1C1 ∠ CAB = ∠ C1A1B1, ∠ ABC = ∠ A1B1C1. Докажем, что Δ ABC подобен Δ A1B1C1.
Пусть k = AB/A1B1. Подвергнем Δ A1B1C1 гомотетии с коэффициентом k. Получится некоторый Δ A2B2C2.
Δ A2B2C2 = Δ ABC по второму признаку равенства треугольников (∠ C2A2B2 = ∠ C1A1B1 = ∠ CAB, ∠ A2B2C2 = ∠ A1B1C1 = ∠ ABC так как преобразование подобия сохраняет углы, A2B2 = k*A1B1 = AB, по условию).
Треугольники A1B1C1 и A2B2C2 гомотетичны, следовательно подобны. Δ A2B2C2 = Δ ABC, следовательно подобны тоже, а значит треугольники A1B1C1 и ABC подобны. Теорема доказана12 билет

1) Необходимое и достаточное условие коллинеарности векторов a = (x, y, z) и b = (u, v, w):

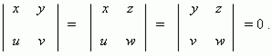Необходимое и достаточное условие компланарности векторов a = (x, y, z), b = (u, v, w) и c = (p, q, r):

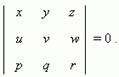
П р и м е р. Даны векторы: a = (1, 2, 3) и b = (– 2, 0,4).

Вычислить их скалярное и векторное произведения и угол

между этими векторами.

Р е ш е н и е. Используя соответствующие формулы (см. выше), получим:

a). скалярное произведение:

(a, b) = 1 · (– 2) + 2 · 0 + 3 · 4 = 10;

б). векторное произведение:

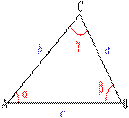
Теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Теорема Пифагора это частный случай теоремы косинусов о которой я поведу речь. Теорема косинусов имеет вид: a² = b² + c² - 2bc*Cos(A) Cos(A) это угол лежаший напротив стороны a (обычное обозначение сторон и углов: напротив стороны "а" лежит угол A, "b" лежит угол B, "c" лежит угол C). Доказательство теоремы не очень сложное, судите сами: Введем систему координат с началом в точке А так, как показано на рисунке. Тогда точка В имеет координаты (с;0), а точка С - (b cos A; b sin A). По формуле расстояния между двумя точками получаем ВС² = а² = (b cos(A) - c)² + b²Sin²(A) = = b²Cos²(A) + b²Sin²(A) - 2*bcCos(A) + c² = = b² + c² - 2*bcCos(A) Теорема доказана.

13 билет

1. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы либо одинаково направлены, либо противоположно направлены.

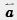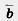Пусть и — отличные от нуля коллинеарные векторы. Докажем, что существует число 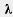такое, что

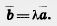
Допустим, векторы 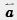и 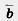одинаково направлены. Векторы

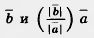
одинаково направлены и имеют одну и ту же абсолютную величину | 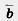|. Значит, они равны:

В случае противоположно направленных векторов 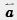и 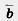аналогично заключаем, что

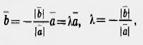что и требовалось доказать.

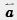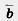Пусть и — отличные от нуля неколлинеарные векторы. Докажем, что любой вектор с можно представить в виде

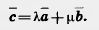
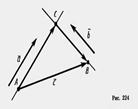
Пусть А и В — начало и конец вектора 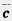(рис. 224). Проведем через точки А и В прямые, параллельные векторам 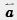и 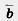. Они пересекутся в некоторой точке С. Имеем:

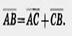
Так как векторы 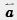и 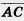коллинеарны, то 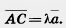. Так как векторы 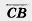и 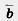коллинеарны, то 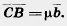. Таким образом,

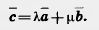
что и требовалось доказать.

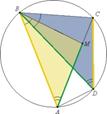
Теорема Птолемея Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон. В четырехугольнике ABCD, вписанном в окружность, AC ∙ BD = AB ∙ CD + BC ∙ AD.

Отметим на AC точку M такую, что 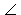ABM = 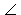DBC. Т. к. вписанные углы BDC и BAC опираются на одну и ту же хорду BC, они тоже равны друг другу. Таким образом, треугольники BDC и BAM подобны, а значит, CD / BD = MA / BA, или, перемножая крест на крест, MA ∙ BD = AB ∙ CD.

В то же время 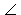ABD = 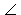MBC (т. к. 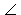ABM = 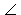DBC), а 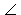BCA = 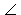BDA, как опирающиеся на одну хорду AB. Значит, AD / BD = MC / BC, или, перемножая крест на крест, MC ∙ BD = AD ∙ BC.

Складывая почленно равенства MA ∙ BD = AB ∙ CD и MC ∙ BD = AD ∙ BC, получаем (MA + MC) ∙ BD = AB ∙ CD + AD ∙ BC, или AC ∙ BD = AB ∙ CD + BC ∙ AD, что и требовалось доказать.

Теперь выведем формулу синуса суммы углов.

Пусть 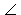AOC = 2α, а 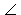AOD = 2β, тогда 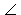COD = 2 (α + β).

AC = 2 R sin α, AD = 2 R sin β,

Согласно вышеприведенным формулам для хорд, стягивающих углы,

CD = 2 R sin (α + β),

BC = 2 R cos α, BD = 2 R cos β,

и, на основании теоремы Птолемея,

AB ∙ CD = AC ∙ BD + BC ∙ AD,

2 R ∙ 2 R sin (α + β) = 2 R sin α ∙ 2 R cos β + 2 R cos α ∙ 2 R sin β,

отсюда и получаем:

А теперь выведем формулу для синуса разности углов.

Пусть 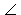AOB = 2α, а 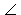AOD = 2β, тогда 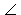BOD = 2 (α – β).

Согласно вышеприведенным формулам для хорд, стягивающих углы,

AB = 2 R sin α, AD = 2 R sin β,

BD = 2 R sin (α – β),

BC = 2 R cos α, CD = 2 R cos β.

И, на основании теоремы Птолемея,

2 R sin α ∙ 2 R cos β = 2 R ∙ 2 R sin (α – β) + 2 R cos α ∙ 2 R sin β,

sin (α – β) = sin α ∙ cos β – cos α ∙ sin β.

отсюда и получаем:

sin (α + β) = sin α ∙ cos β + cos α ∙ sin β.

14 билет

1) Скалярным произведением двух векторов и называется число, обозночаемое и равное произведению модулей данных векторов на косинус угла между ними:

a•b=|a|•|b|•cos(a^b)

где (a^b) обозначает меньший угол между направлениями векторов a и b. Отметим, что всегда(0≤a^b≤π).

Основные свойства скалярного произведения векторов:
1. a •b = b• a;
2. (λa)•b= •(λb) = λ (a•b);
3. a•(b+с) = a•b+a•с;
4. a•b = | a | прa b = |b| прb| a |;
5. a • a = | a |²;
6. a • b = 0, если a ┴ b.

Если a =(x₁, y₁, z₁), b =(x₂, y₂, z₂), то в базисе (i, j, k):
a • b = x₁x₂+ y₁y₂ +z₁z₂, | a | = √x1²+ y1²+ z1², | b | = √x2²+ y2²+ z2².

2) Теорема

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.