Параллелограмм. Свойства параллелограмма с доказательством

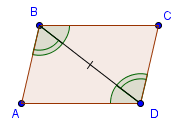
Определение. Параллелограмм – это четырёхугольник, противоположные стороны которого попарно параллельны.

Свойство 1. Любая диагональ параллелограмма делит его на два равных треугольника.

Доказательство. По II признаку (накрест лежащие углы и общая сторона).

Теорема доказана.

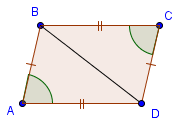
Свойство 2. В параллелограмме противолежащие стороны равны, противолежащие углы равны.

Доказательство.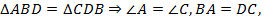
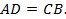Аналогично,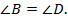

Теорема доказана.

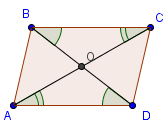
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.

Доказательство.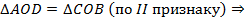

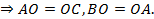
Теорема доказана.

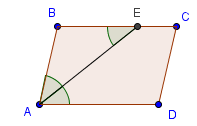
Свойство 4. Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. – вершину – два равнобедренных?-ка).

Доказательство.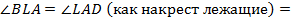

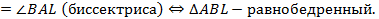
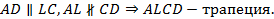
Теорема доказана.

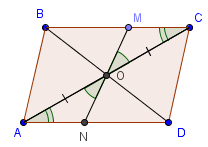
Свойство 5. В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.

Доказательство.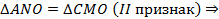

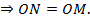
Теорема доказана.

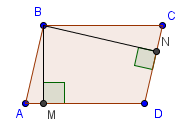
Свойство 6. Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.

Доказательство.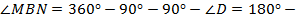

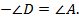
Теорема доказана.

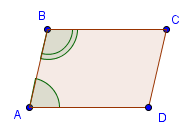
Свойство 7. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Доказательство.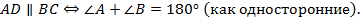

Теорема доказана.

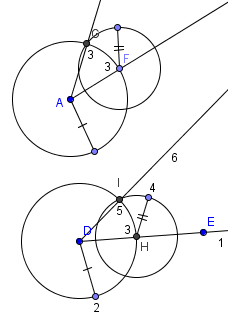
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.

1) Построить произвольный луч DE.

2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.

3) F и G – точки пересечения окружности со сторонами данного угла, H – точка пересечения окружности с построенным лучом

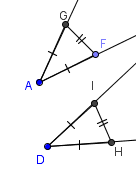
Построить окружность с центром в точке H и радиусом, равным FG.

5) I – точка пересечения окружностей построенного луча.

6) Провести прямую через вершину и I.

IDH – требуемый угол.
(
)

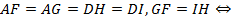
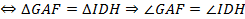Свойство 1. Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.

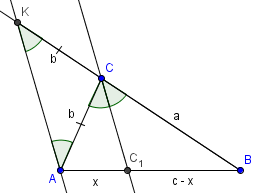
Доказательство. Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.

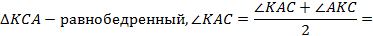
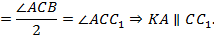
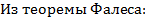
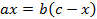
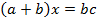
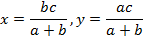
Теорема доказана.

Свойство 2. Биссектриса – ГМТ равноудалённых от прилежащих сторон треугольника.

Свойство 3. Биссектрисы треугольника пересекаются в одной точке, и эта точка – центр вписанной окружности треугольника. (Из предыдущего свойства)

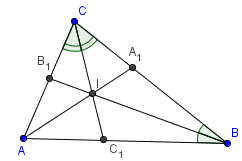
Свойство 4. Биссектрисы делятся точкой пересечения в отношении суммы прилежащих сторон к противолежащей стороне, считая от вершины.

Доказательство. Рассмотрим треугольник CBC₁:

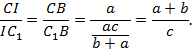
Теорема доказана.