2015-04-12
6590
1) 
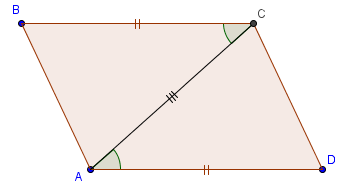Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Доказательство. Пусть в четырёхугольнике АВСD стороны АD и СB параллельны и равны. Проведём диагональ АС, делящую параллелограмм на два треугольника: АВС и СDА. Эти треугольники равны по первому признаку, значит, их соответствующие углы равны. Тогда углы BAC и DCA равны как внутренние накрест лежащие при пересечении прямых АB и CD секущей АС, значит, АB||CD. Следовательно, АВСD – параллелограмм.
2) 
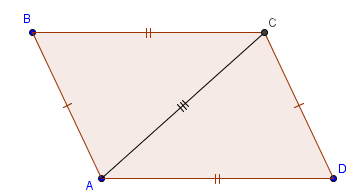Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Доказательство. Проведём диагональ АС данного четырёхугольника АВСD, делящую его на треугольники АВС и СDА. Эти треугольники равны по третьему признаку, поэтому углы АCВ и СAD равны, значит АВ||CD. Т.к. АВ и СD равны и параллельны, то по первому признаку АВСD – параллелограмм.
3) 
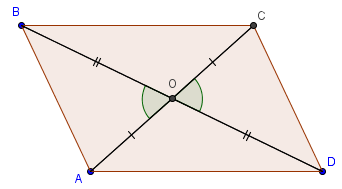Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся напополам, то этот четырёхугольник – параллелограмм.
Доказательство.
.
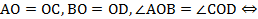
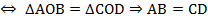Аналогично,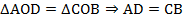 
.
Противоположные стороны попарно равны, значит, ABCD – параллелограмм.
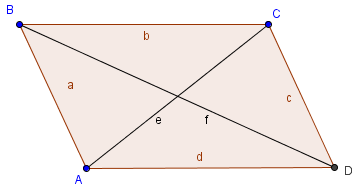
4) В параллелограмме удвоенная сумма квадратов сторон равна сумме квадратов диагоналей:
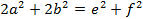
Доказательство.
Воспользуемся теоремой косинусов:
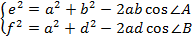
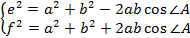
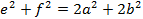
Теорема доказана.
2. 
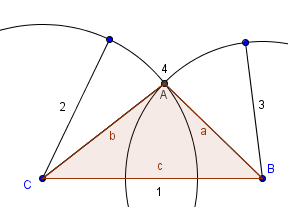Построение треугольника по трём сторонам.
1) Отложить на плоскости отрезок BC=a.
2) Построить окружность с центром в точке B с радиусом c.
3) Построить окружность с центром в точке C
с радиусом b.
4) Отметить точку A – одно из пересечений окружностей.
ABC – требуемый треугольник.
