А10. Циклическая перестановка сомножителей не меняет смешанного произведения, т.е. 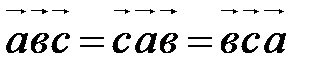
 V.
V.
Перестановка двух соседних сомножителей меняет знак смешанного произведения на противоположный, т.е.
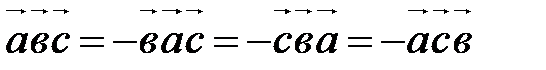 ,
,  V.
V.
Для доказательства достаточно применить доказательство свойства Г20 к 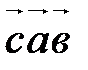 и к
и к 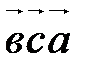 . Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах
. Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах 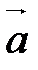 и
и 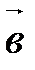 , во втором – на векторах
, во втором – на векторах 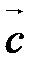 и
и 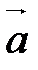 ).
).
Чтобы доказать вторую часть свойства, надо воспользоваться определением смешанного произведения и свойством А10 векторного умножения, а затем совершить циклическую перестановку:
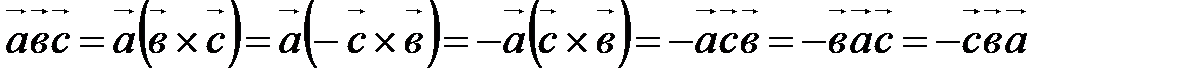 .
.
А20. 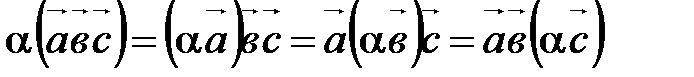
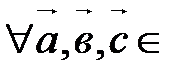 V
V 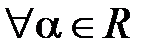 .
.
Для доказательства этого свойства нужно доказать три равенства:
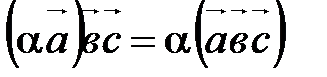 ;
; 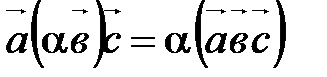 ;
; 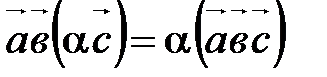 .
.
Докажите их самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов.
А30. 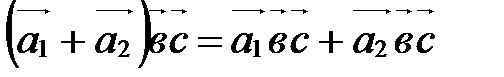 ;
;
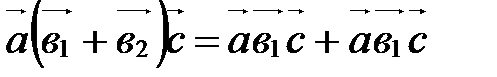 ;
;
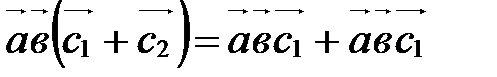 .
.
Докажите эти равенства самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов.
Замечание. Смешанное произведение 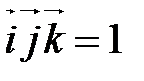 .
.
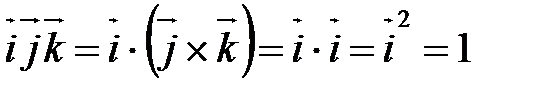 , т.к.
, т.к. 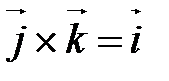 .
.
Теорема 1(смешанное произведение в координатах). Если 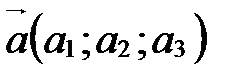 ,
, 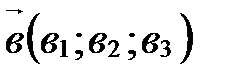 ,
, 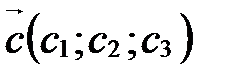 в базисе
в базисе 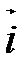 ,
, 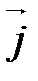 ,
, 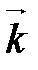 , то
, то 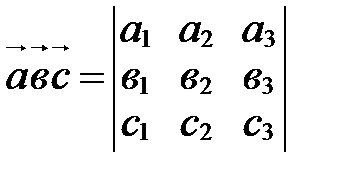 .
.
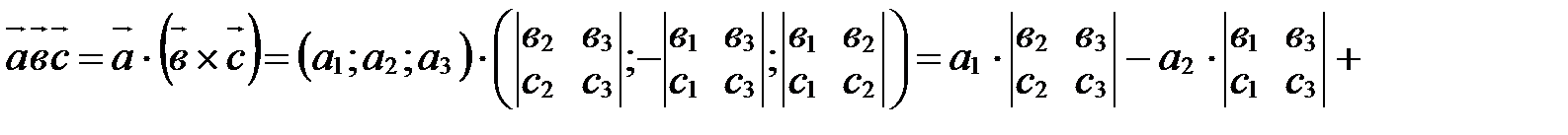
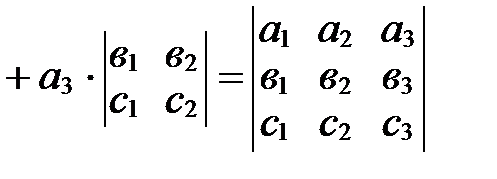 .
.
 2015-04-12
2015-04-12 1063
1063








