СБОРНИК ЗАДАЧ
ПО КУРСУ
«НАЧЕРТЕТЕЛЬНАЯ ГЕОМЕТРИЯ»
(Для студентов всех специальностей)
Учебно-методическое пособие
Череповец
ВВЕДЕНИЕ
Для закрепления теоретического материала в данном учебно-методическом пособии предлагаются задачи по основным разделам начертательной геометрии:
§ точка;
§ прямая;
§ плоскость;
§ взаимное расположение элементов пространства относительно плоской проекции;
§ взаимное расположение прямых, плоскостей, прямой и плоскости.
Разделы пособия соответствуют разделам теоретического курса и включают задачи как метрические (определение натуральной величины углов, расстояний, плоских фигур), так и позиционные (построение прямых, плоскостей и поверхностей в заданном положении относительно плоскостей проекций и друг друга).
Терминология, обозначения и сокращения, используемые в данном пособии, соответствуют терминологии, принятой в курсе лекций и используемой на практических занятиях по дисциплине «Инженерная и машинная графика» на кафедре инженерной и машинной графики ЧГУ.
Т е м а 1
ТОЧКА
Контрольные вопросы
1. Как принято обозначать плоскости проекции?
2. Что называют осью проекции?
3. Что такое эпюр точки и как перейти от пространственного чертежа к эпюру?
4. Какая координата определяет расстояние точки до плоскости проекции 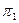 ,
, 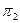 ,
, 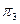 ?
?
5. Как построить эпюр точки в разных октантах?
1.1 Построить наглядное изображение и эпюр по заданным координатам: А (40, 45, 25); В (30, 35, 0); С (0, 25, 20); D (10, 0, 0); Е (20, 0, 15).
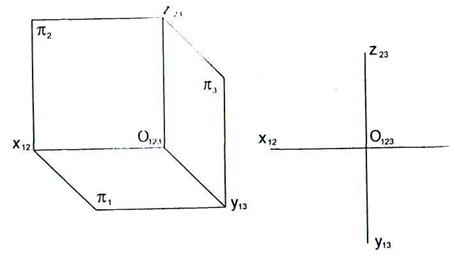
1.2 Построить центральную проекцию 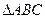 , параллельного плоскости
, параллельного плоскости 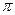 (S – центр проектирования, А1 – проекция точки А на плоскости
(S – центр проектирования, А1 – проекция точки А на плоскости 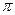 ).
).
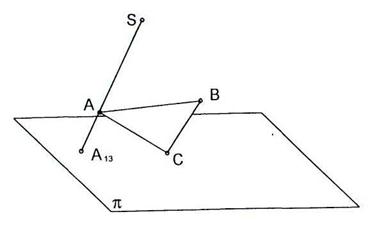
1.3 Достроить наглядное изображение и построить эпюр точек А, В, С. Записать их координаты.
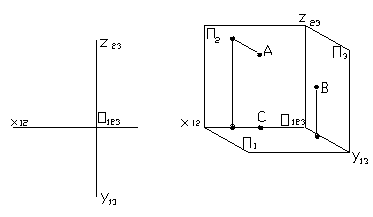
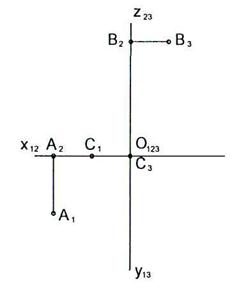
1.4 По двум данным проекциям точек А, В, С построить их третью проекцию и указать положение точек в пространстве.
1.5 Точка А удалена от плоскости 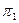 на 30 мм, от плоскости
на 30 мм, от плоскости 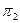 - на 20 мм. Определить положение осей проекции и построить третью проекцию точки.
- на 20 мм. Определить положение осей проекции и построить третью проекцию точки.

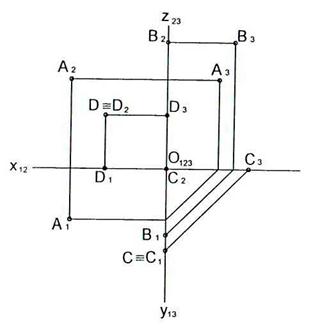
1.6 Дан эпюр точек A, B, C, D. Записать их координаты и положение относительно плоскостей проекций.
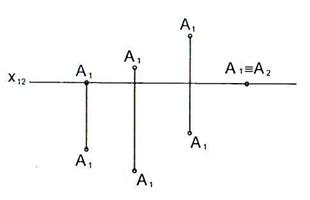
1.7 На каком чертеже изображена точка А, равноудаленная от плоскостей 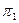 и
и 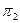 ?
?
1.8 Какая из точек - A, B, C, D – принадлежит плоскостям 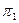 и
и 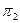 ?
?
Координаты точек: А (5, 10, 20); В (15, 10, 0); С (30, 0, 40); D (0, 10, 15).
1.9 Какая из указанных на чертеже точек принадлежит плоскости 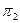 ?
?
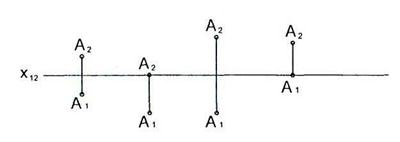
1.10 Какая из указанных на чертеже точек принадлежит Х12?
Точки имеют координаты: А (15, 0, 0); В (0, 10, 15); С (15, 10, 0); D (10, 20, 30).
1.11 Какая из указанных на чертеже точек наиболее удалена от плоскости 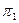 ? Определить положение этих точек в пространстве.
? Определить положение этих точек в пространстве.
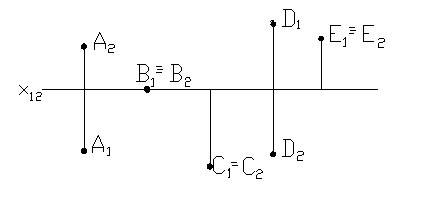
1.12 Какая из указанных на чертеже точек ближе к плоскости 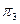 ?
?
Т е м а 2
ПРЯМАЯ ЛИНИЯ
Контрольные вопросы
1. Дайте определение линии и отрезка линии.
2. Какая прямая линия называется прямой общего положения?
3. Какие частные положения прямой линии могут быть относительно плоскостей проекции?
4. Как разделить отрезок прямой линии на эпюре в заданном отношении?
5. Что называется следом прямой?
6. Сколько следов имеют прямые общего положения, прямые уровня, проецирующие прямые?
7. Как могут быть взаиморасположены в пространстве две прямые?
8. Как отличить на эпюре пересекающиеся прямые линии от скрещивающихся?
9. Что такое конкурирующие точки? Для чего их используют?
10. В каком случае точка принадлежит прямой?
2.1 Построить на эпюре три проекции отрезка АВ по заданным координатам его концов: А (25, 20, 5) и В (5, 10, 30). Разделить отрезок АВ точкой С в отношении 2: 5.
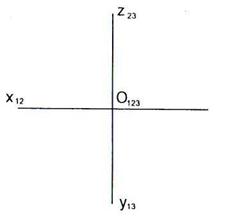
2.2 Построить отрезок прямой [ АВ ] по заданным координатам его концов: А (10, 25, 10), В (40, 5, 25) – в пространстве и на эпюре.
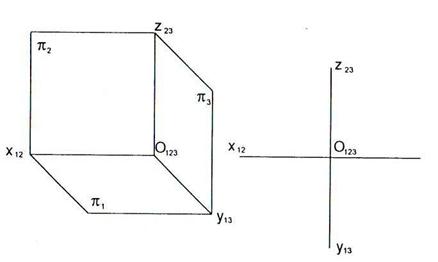
2.3 Через точку А провести горизонтальную прямую под углом 300 к плоскости 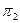 и отложить на ней отрезок АВ = 25 мм. Найти на этом отрезке точку С, отстоящую от плоскости
и отложить на ней отрезок АВ = 25 мм. Найти на этом отрезке точку С, отстоящую от плоскости 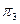 на 20 мм.
на 20 мм.
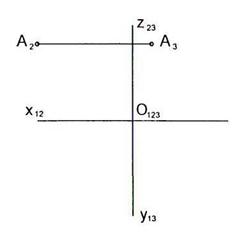
2.4 Даны проекции точки А. Построить три проекции отрезка АВ длиной 25 мм, перпендикулярного плоскости 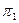 , и три проекции отрезка АС длиной 20 мм, перпендикулярного плоскости
, и три проекции отрезка АС длиной 20 мм, перпендикулярного плоскости 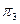 .
.
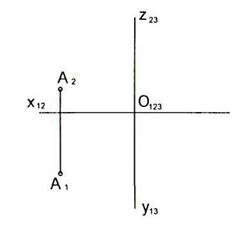
2.5 Построить горизонтальную проекцию точки А, лежащей на отрезке ВС. Решить задачу двумя способами: делением отрезка в заданном отношении, с помощью построения третьей проекции.
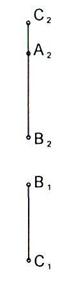
2.6 Построить на эпюре горизонтальную проекцию отрезка АВ, недостающие проекции точки С, принадлежащей отрезку АВ, и проверить, принадлежит ли точка К этому отрезку.
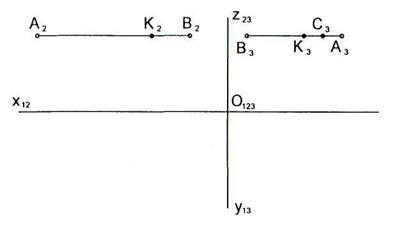
2.7 Построить фронтальную проекцию отрезка АВ, лежащего во фронтальной плоскости 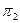 . АВ = 30 мм.
. АВ = 30 мм.
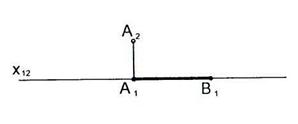
2.8 Построить горизонтальную проекцию отрезка АВ ½½ 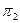 . АВ = 40 мм.
. АВ = 40 мм.
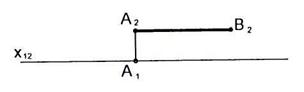
2.9 Отрезок АВ = 30 мм, АВ ½½ 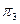 . Определить А2В2, А3В3.
. Определить А2В2, А3В3.
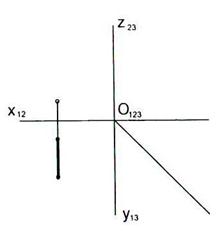
2.10 На каком чертеже изображена фронтальная прямая?
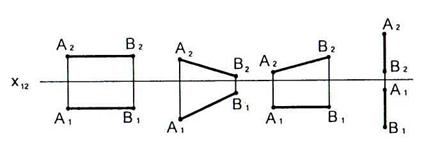
2.11 На каком чертеже изображена профильная прямая?
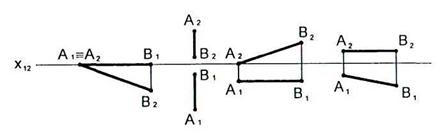
2.12 На каком чертеже изображена горизонтальная прямая?
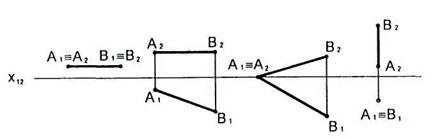
2.13 На каком чертеже изображена фронтально проецирующая прямая?
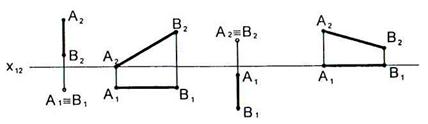
2.14 На отрезке ВС определить: точку А, удаленную от плоскости 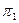 на 25 мм, точку D, удаленную от плоскости
на 25 мм, точку D, удаленную от плоскости 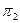 на 20 мм, точку Е, равноудаленную от плоскостей
на 20 мм, точку Е, равноудаленную от плоскостей 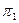 и
и 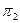 .
.
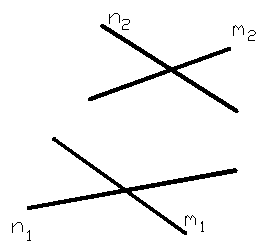
2.15 Выяснить взаимное расположение прямых m и n. Указать конкурирующие точки.
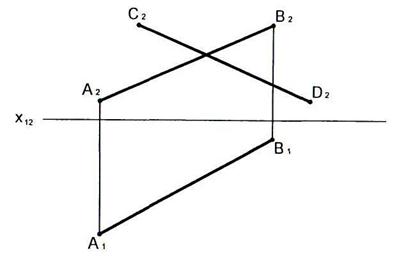
2.16 Построить горизонтальную проекцию отрезка СD, параллельного плоскости 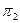 и отстоящего от нее на 25 мм. Определить конкурирующие точки отрезков АВ и CD.
и отстоящего от нее на 25 мм. Определить конкурирующие точки отрезков АВ и CD.
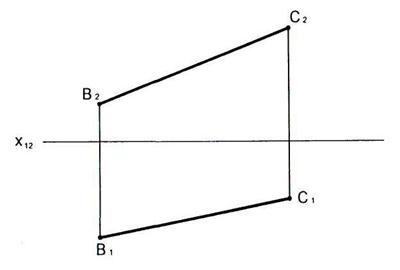
2.17 Построить горизонтальный и фронтальный следы прямой АВ и указать, через какие четверти пространства она проходит.
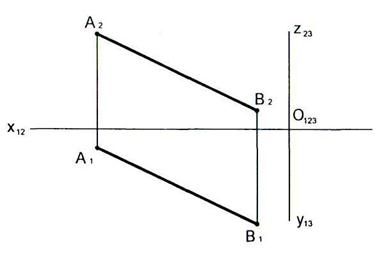
2.18 Построить следы прямой АВ.
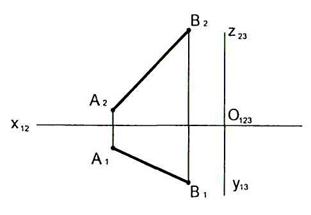
2.19 Построить следы прямой АВ.
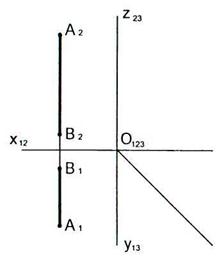
2.20 Построить следы прямой АВ.
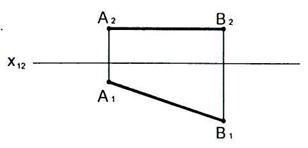
2.21 Построить следы прямой АВ.
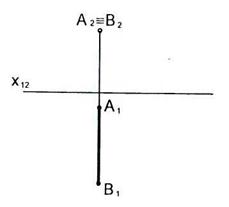
2.22 Построить следы прямой АВ.
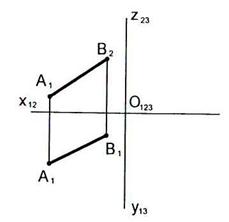
2.23 На каком чертеже изображены параллельные прямые?
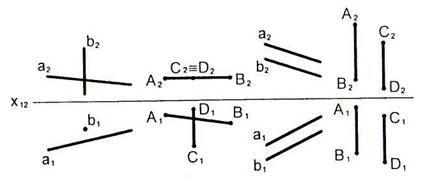
2.24 На каком чертеже изображены пересекающиеся прямые?
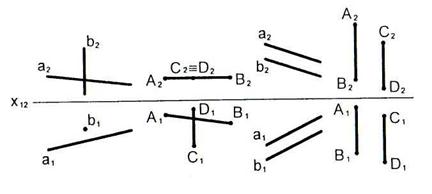
2.25 На каком чертеже изображены скрещивающиеся прямые?
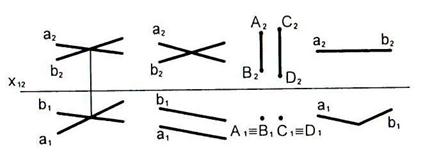
2.26 Указать взаимное положение прямых. Определить расстояние между ними.
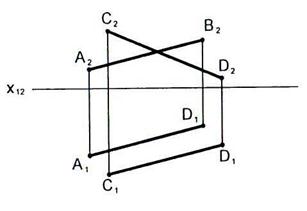
2.27 Через точку Е провести прямую, пересекающую прямые СD и АВ.
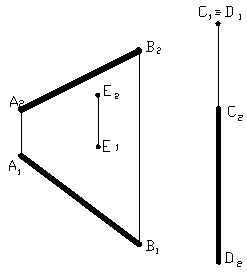
2.28 Определить расстояние между прямыми YL и EK.
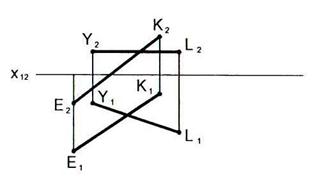
2.29 Определить расстояние между скрещивающимися прямыми.
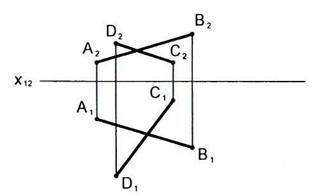
2.30 Выяснить взаимное расположение прямых.
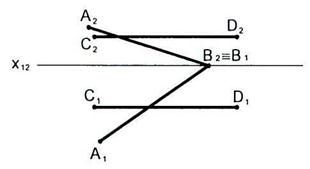
2.31 Выяснить взаимное расположение прямых.
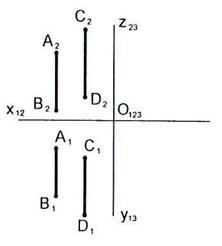
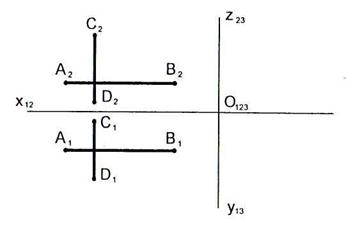
2.32 Выяснить взаимное расположение прямых.
Т е м а 3
 2015-04-12
2015-04-12 2508
2508
