Тригонометрические функции углового аргумента

Из геометрии известно, что синус (косинус) острого угла — это отношение катета прямоугольного треугольника к его гипотенузе, а тангенс (котангенс) угла — это отношение катетов прямоугольного треугольника. Иной подход к понятиям синуса, косинуса, тангенса и котангенса развивали мы в предыдущих параграфах. На самом деле эти подходы взаимосвязаны, в чем мы сейчас убедимся.

Возьмем угол с градусной мерой <х° и расположим его в модели «числовая окружность в прямоугольной системе координат» так, как показано на рис. 112: вершину угла совместим с центром окружности (с началом системы координат), а одну сторону угла совместим с положительным лучом оси абсцисс. Точку пересечения второй стороны угла с окружностью обозначим буквой М. Ординату точки М естественно считать синусом угла а°, а абсциссу этой точки — косинусом угла а°.

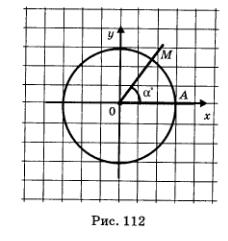
Для отыскания синуса или косинуса угла а° совсем не обязательно каждый раз делать указанные весьма сложные построения. Достаточно заметить, что дуга АМ составляет такую же часть длины числовой окружности, какую угол а составляет от угла 360°. Если длину дуги АМ обозначить буквой то получим:

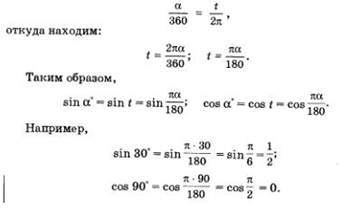
Считают, что 30° — это градусная мера угла, а

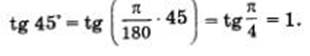
Угол в 1 радиан — 360 это центральный угол, опирающийся на дугу длиной 1, т.е. на дугу, длина которой равна радиусу 180° окружности.

Рассматривая функцию u = sin t (или любую другую тригонометрическую функцию ), мы можем считать независимую переменную t числовым аргументом, как это было в предыдущих параграфах, но можем считать эту переменную и мерой угла, т.е. угловым аргументом. Поэтому, говоря о тригонометрической функции, в определенном смысле безразлично считать ее функцией числового или углового аргумента.

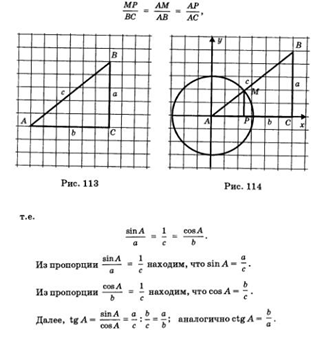
Доказательство. Совместим прямоугольный треугольник АВС с числовой окружностью так, как показано на рис. 114: вершину А поместим в центр окружности, катет АС «пустим» по положительному направлению оси абсцисс. Точку пересечения гипотенузы АВ с окружностью обозначим буквой М. Опустим из точки М перпендикуляр МР на прямую АС. Заметим, что АР и МР — абсцисса и ордината точки М, т.е. АР = соз А, МР = зш А. Учтем также, что АМ = 1 (радиус числовой окружности равен 1) и что АВ = с, АС = Ь, ВС = а.
Так как треугольники АМР и АВС подобны, то

13. Формулы приведения.

1) Если под знаком преобразуемой тригонометрической функции содержится выражение π+t, π-t, 2π+t или 2π-t, то наименование тригонометрической функции следует сохранить.

2) Если под знаком преобразуемой тригонометрической функции содержится выражение п/2+t, п/2-t, 3п/2+t, 3п/2-t, то наименование тригонометрической функции следует изменить на родственное

3) Епред полученной ф-ей от аргумента t надо поставить тот знак, который имела бы преобразуемая ф-ия при условии, что 0<t<п/2.

Это правило используется и в том случае, когда аргумент задан в градусах.

15. Сечения многогранников.

Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранником. Примеры многогранников: тетраэдр, параллелепипед, октаэдр.

Многоугольники, из которых составлен многогранник, называются его гранями. Грани тетраэдра и октаэдра – треугольники, параллелепипеда – параллелограммы. Стороны граней – ребра, концы ребер – вершины. Отрезок, соед. 2 вершины, не принадлежащие одной грани, называется диагональю многогранника. Плоскость, по обе стороны от которой имеются точки многогранника, называется секущей плоскостью, а общая часть многогранника и секущей плоскости – сечением многогранника. Многогранники бывают выпуклыми и невыпуклыми.

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;