УДК 515.0 (075.8) ББК 22.151.3
Рецензенты:
главный инженер ЗАО «Рязаньгражданпроект»,
кандидат технических наук Л.А. Нудельман;
заведующий кафедрой «Начертательная геометрия и графика»
Московского государственного строительного университета,
профессор Т.М. Кондратьева;
профессор кафедры начертательной геометрии и инженерной графики
ГОУ ВПО ВГАСУ В. П. Каминский.
Рудомин Е.Н., Рудомина Н.Я., Бодрова Н.Н.
Сборник задач по начертательной геометрии в ортогональных проекциях и в проекциях с числовыми отметками: Учебное пособие. - М: Издательство Ассоциации строительных вузов, 2005 г. - 160 с.
ISBN 5-93093-381-2
В Сборнике представлены задачи по начертательной геометрии в ортогональных проекциях и в проекциях с числовыми отметками с кратким содержанием пояснений к темам применительно к программе строительных специальностей высших учебных заведений. В конце каждого раздела приведены вопросы для самопроверки.
Сборник задач может служить учебным пособием для студентов всех форм обучения строительных специальностей при решении задач на практических занятиях, а также при выполнении индивидуальных заданий.
ISBN 5-93093-381-2
© Издательство АСВ, 2005
© Рудомин Е.Н., Рудомина Н.Я., Бодрова Н.Н., 2005
ПРЕДИСЛОВИЕ
Сборник задач предназначен для студентов строительных специальностей высших учебных заведений.
Содержание учебного пособия соответствует программе по начертательной геометрии для студентов строительных специальностей.
В данном учебном пособии рассматриваются позиционные, метрические и конструктивные задачи и задачи на построение аксонометрических проекций.
Структура учебного пособия состоит из двух видов проецирования - ортогональное проецирование и проекции с числовыми отметками. В каждом разделе представлено по видам проецирования краткое содержание основных понятий и определений с поясняющими рисунками, как в аксонометрии, так и в проекциях на плоскостях проекций.
В разделах приведены задачи в ортогональных проекциях и в проекциях с числовыми отметками, которые помогут студентам получить знания и их применить при изучении таких дисциплин как «Инженерная геодезия», «Водоснабжение и водоотведение», «Архитектура гражданских и промышленных зданий и сооружений», «Технология строительных процессов», Технология возведения зданий и сооружений», «Реконструкция зданий и сооружений» и др.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ и символика
| Знак | Содержание | Пример чтения символической записи |
| Точка | Прописные буквы латинского алфавита или цифры | А, B, C или 1, 2, 3 |
| Линии | Строчные буквы латинского алфавита | а, в, c, d |
| Плоскость, поверхность, угол | Строчные буквы греческого алфавита | 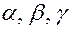
|
| Проекции геометрических фигур | Те же буквы только с соответствующими индексами плоскостей проекций | Проекции точки А1, A2,
линии l1, l2,
угла 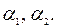
|
| = | результат действия | |
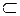
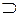
| принадлежность, включение | b 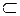 α - прямая b принадлежит
плоскости α α - прямая b принадлежит
плоскости α
|
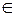
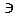
| принадлежность, включение точки во множество | 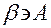 - точка А принадлежит
плоскости β - точка А принадлежит
плоскости β
|
| U | Объединение, соединение | A U B = b - прямая соединяет точки А, B |
| ∩ | пересечение | К = b ∩ α - точка К есть результат пересечения прямой b с плоскостью α |
| U | касание | a U γ - прямая a касается поверхности γ |
| ║ | параллельность | d ║ 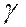 - прямая d параллельна
плоскости γ - прямая d параллельна
плоскости γ
|
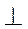
| перпендикулярность | b 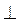 a - прямая b перпендикулярна
прямой a a - прямая b перпендикулярна
прямой a
|
| _ · _ | скрещивание | m · n – прямые m и n скрещиваются |
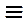
| совпадение | А 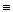 В – точки А и В совпадают В – точки А и В совпадают
|
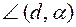
| Величина угла | 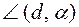 - величина угла между прямой d и плоскостью α - величина угла между прямой d и плоскостью α
|
| ↔ | эквивалентность | р 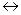 q - если р, то и q;- если q, то и р. q - если р, то и q;- если q, то и р.
|
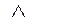
| коньюкция предложений, союз «и» | 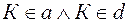 точка К принадлежит прямым a и d точка К принадлежит прямым a и d
|
ИНВАРИАНТНЫЕ (НЕИЗМЕНЯЕМЫЕ) СВОЙСТВА ПАРАЛЛЕЛЬНОГО ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
· Проекции точки - точка
А ↔ А1 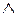 А2 .
А2 .
· Проекции прямой линии - прямая
а ↔ а1 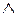 а2 .
а2 .
· Если точка принадлежит прямой, то проекции точки принадлежат проекции прямой:
А 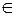 а ↔ А1
а ↔ А1 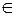 а1
а1 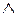 А2
А2 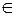 а2.
а2.
· Если точка С делит отрезок [ АВ] в отношении 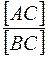 , то проекции этого отрезка делятся в том же отношении:
, то проекции этого отрезка делятся в том же отношении:
С 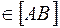
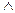
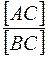 =
= 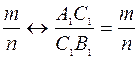
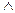
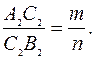
· Если отрезки параллельны и находятся в каком-то отношении, то проекции их тоже параллельны и находятся в том же отношении:
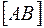 ║
║ 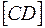
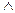
 ↔ А1 В1 ║ С1D1
↔ А1 В1 ║ С1D1  A2B2 ║ C2D2
A2B2 ║ C2D2 
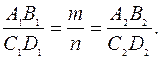
· Если плоскость параллельна плоскости проекции, то проекция ее будет конгруэнтна:
β ║ П↔ βП  β.
β.
· Теорема о проецировании прямого угла
Если одна сторона прямого угла параллельна плоскости проекции, а другая не перпендикулярна ей, то прямой угол проецируется в виде прямого угла:
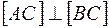
 АС ║ П1, ВС
АС ║ П1, ВС 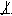 П1↔ А1С1
П1↔ А1С1 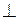 В1С1.
В1С1.
ТОЧКА
 2015-04-12
2015-04-12 287
287







