Тема II. Локальный базис криволинейной системы координат

Пусть М х ¹ х ² х ³ – некоторая криволинейная система координат,
а 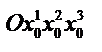– вспомогательная декартова прямоугольная система координат. Известны функции 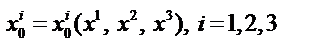, которые связывают, декартовы и криволинейные координаты, тогда локальный базис криволинейной системы координат определим как частные производные радиус-вектора точки по криволинейной координате. Мы получим тройку векторов, зависящих от выбора точки, в которой строится базис. Векторы локального базиса меняют направление и величину при переходе от одной точки к другой.

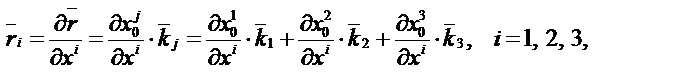
где 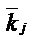– ортонормированный базис декартовой системы координат, т.е.

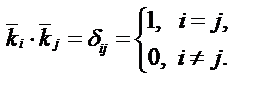
Рассмотрим различные криволинейные системы координат.