Тема IV. Определение тензора

Определение. Экстенсив Q называется m-раз ковариантным и n-раз контравариантным тензором ранга m+n, если его компоненты преобразуются по закону

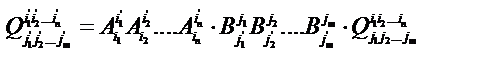
где 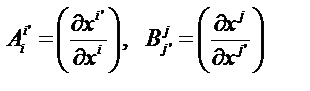– матрицы Якоби преобразования криволинейных координат.

Задача 1. Задан смешанный тензор второго ранга

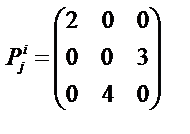
и матрица прямого преобразования криволинейных координат

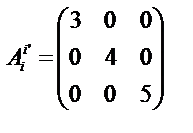. Найдите тензор в новых осях.

Решение. Запишем определение смешанного тензора второго ранга, т.е. закон преобразования его компонент при переходе к новой системе координат

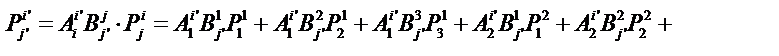
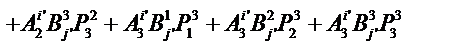
Подставим компоненты тензора в «старых» осях из условия задачи, тогда получим

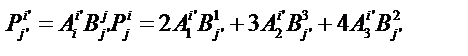
Найдем матрицу обратного преобразования координат, как матрицу обратную к матрице прямого преобразования координат

Определим компоненты тензора в «новых» осях

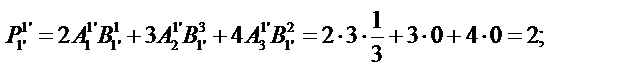
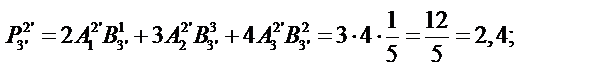
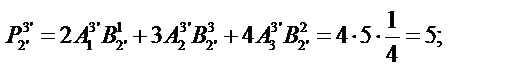
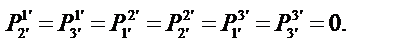
Ответ: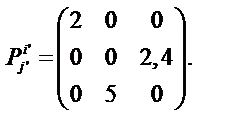

Замечание. Для дважды ковариантного тензора второго ранга и дважды контравариантного тензора второго ранга используются следующие законы преобразования

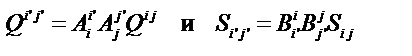
Задача 2. Задан декартов тензор второго ранга 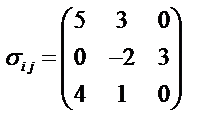Найдите тензор в новых осях, полученных путем поворота старых на угол 45⁰ относительно оси .

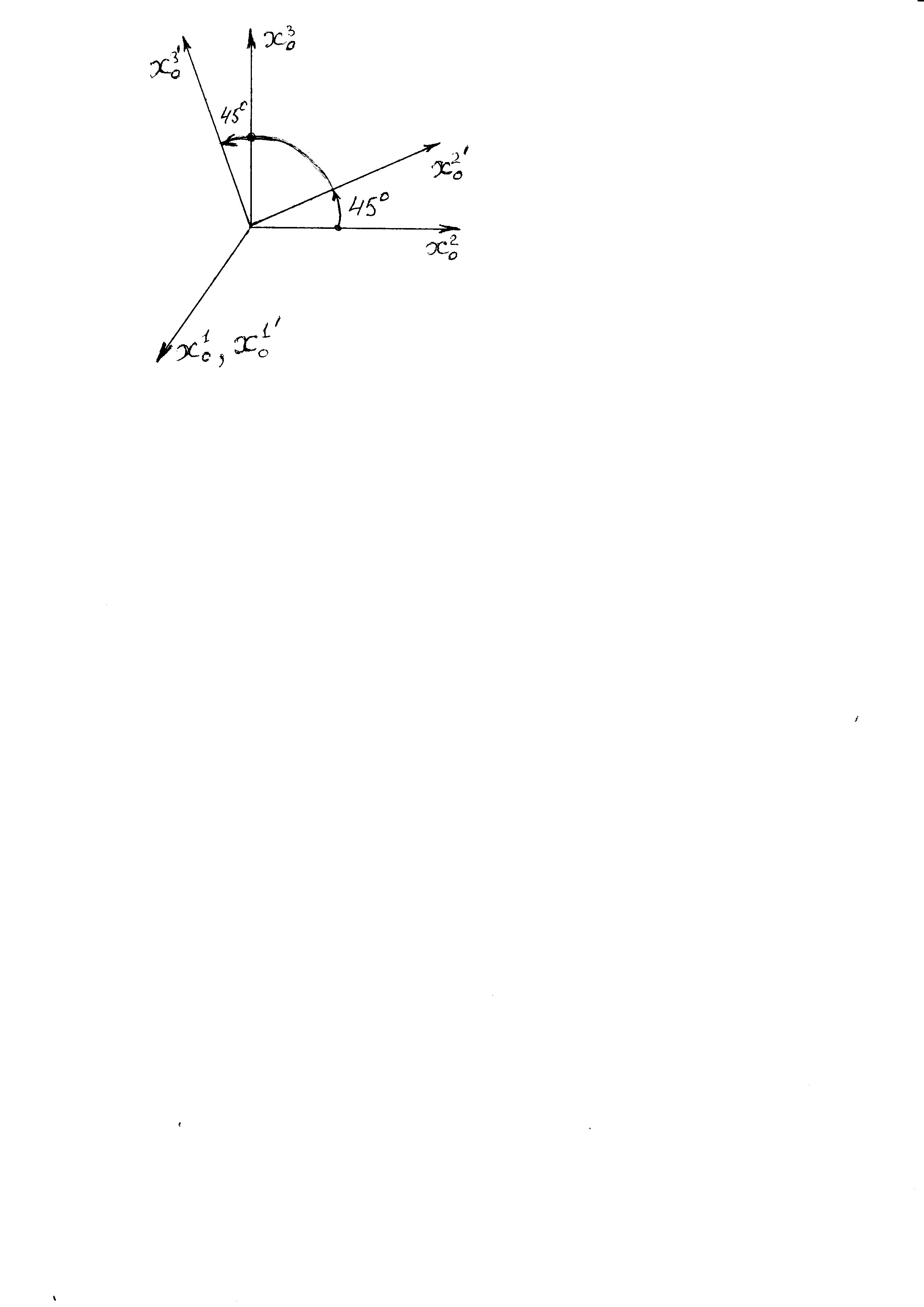
Решение. Определим матрицу преобразования декартовых координат – это матрица косинусов углов межу новыми и старыми осями

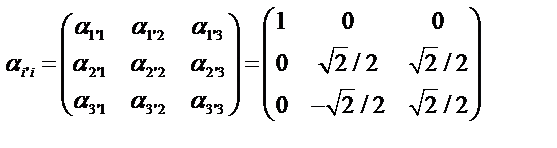
Запишем определение декартового тензора второго ранга

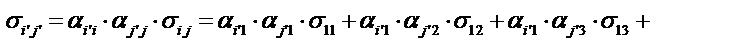
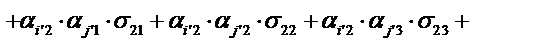
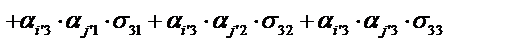
Подставим компоненты тензора в «старых» осях из условия задачи, тогда получим

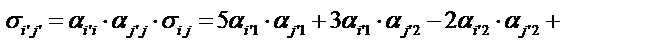
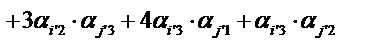
Определим компоненты тензора в «новых» осях

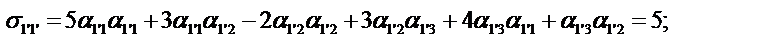
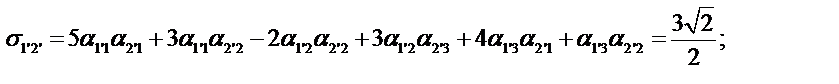
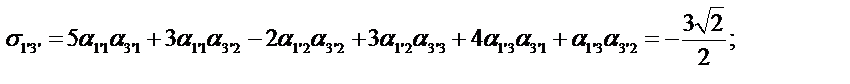
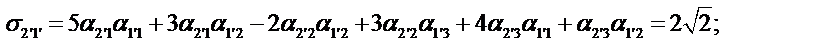
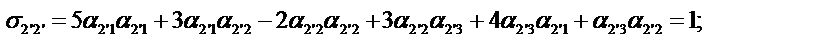
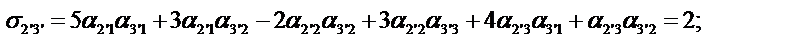
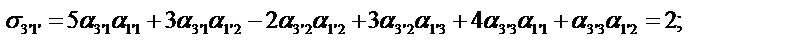
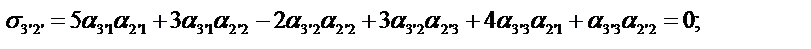
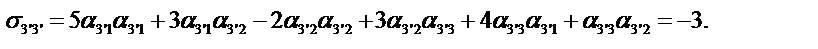
Ответ: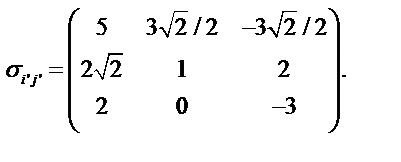

Замечание. В этой задаче важно правильно составить матрицу преобразования декартовых координат при одном повороте относительно других осей 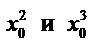. Следует рассмотреть отдельно углы поворота осей 90⁰ и 180⁰.