Повторим операции, которые можно выполнять над тензорами.
1) Сложение тензоров.
В этой операции могут участвовать тензоры одинакового ранга и строения, то есть тензоры с одинаковым числом и чередованием верхних и нижних индексов. В результате мы получаем тензор того же ранга и строения. Тензоры складываются покомпонентно. Например
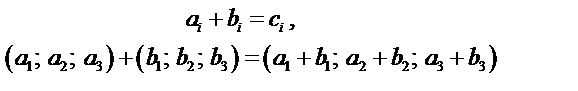
2) Умножение тензора на число.
Каждая компонента тензора умножается на это число, в результате получается тензор того же ранга и строения. Например
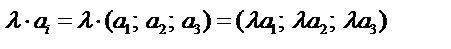
Операция вычитания тензоров выполняется с помощью этих двух операций, т.е. уменьшаемый тензор складывают с вычитаемым умноженным на минус единицу.
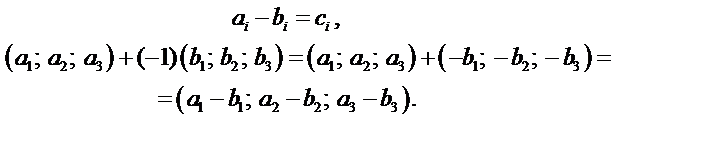
3) Умножение тензоров (внешнее).
В этой операции могут участвовать тензоры любого ранга и строения. Каждая компонента одного тензора умножается на каждую компоненту другого тензора, в результате получается тензор, ранг которого равен сумме рангов сомножителей.
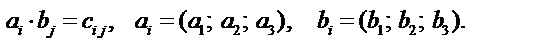
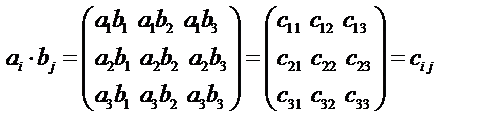
Операция умножения тензоров некоммутативна, т.к.
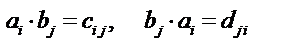
4) Свертка тензора.
В этой операции участвуют тензоры, ранг которых не менее двух. Операция заключается в том, что два свободных индекса тензора обозначаются одной буквой, в результате чего становятся индексом суммирования. Ранг тензора уменьшается на две единицы. Тензор нечетного ранга можно последовательно свернуть до тензора первого ранга. Тензор четного ранга можно последовательно свернуть до тензора нулевого ранга. Свертку тензора можно применять к произведению тензоров, тогда это произведение называют внутренним.
5) Перестановка индексов.
Если два свободных индекса поменять местами, то мы получим тензор того же ранга, с теми же компонентами, но занумерованными в другом порядке. Например
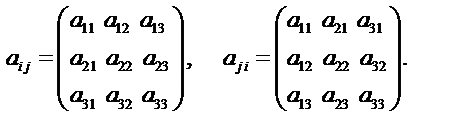
6) Симметрирование тензора.
Симметрирование тензора по двум индексам выполняется по формуле
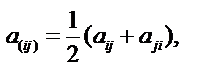
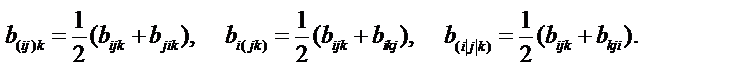
Симметрирование тензора по трем индексам выполняется по формуле
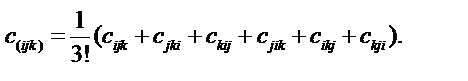
Симметрирование тензора по ‘n’ индексам выполняется по формуле
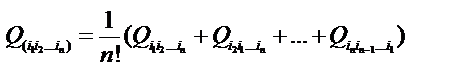
7) Альтернирование тензора (кососимметрирование)
Альтернирование тензора по двум индексам выполняется по формуле
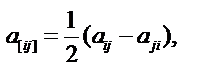
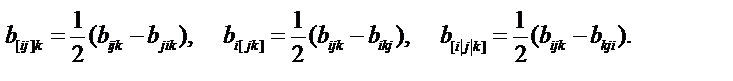
Альтернирование тензора по трем индексам выполняется по формуле
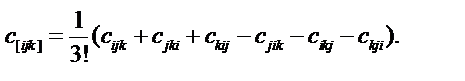
“+” – четная перестановка ijk,
“–” – нечетная перестановка ijk.
Альтернирование тензора по ‘n’ индексам выполняется по формуле
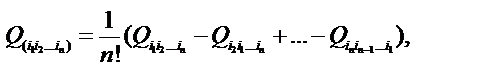
“+” – четная перестановка i1, i2, …,in;
“–” – нечетная перестановка i1, i2, …,in.
Задача 1. Известен тензор второго ранга
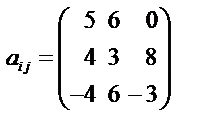
и введены обозначения b ij = a (ij), cij = a [ij]
Определите следующие выражения:
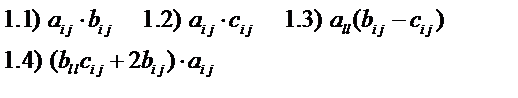
Решение. Определим симметричный и кососимметричный тензоры
b ij и c ij, используя приведенные выше формулы
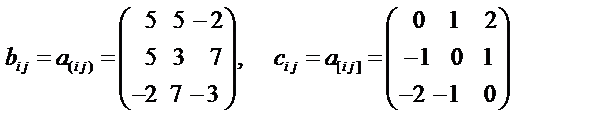
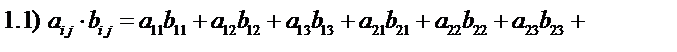
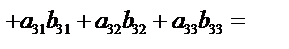 25 + 30 + 20 + 9 + 56 + 8 + 42 + 9 = 199.
25 + 30 + 20 + 9 + 56 + 8 + 42 + 9 = 199.
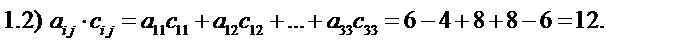
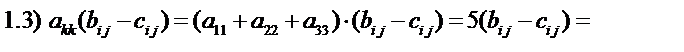
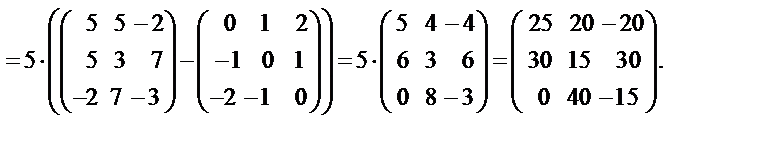
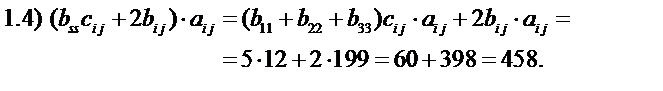
Задача 2. Докажите, что для любого тензора второго ранга ai j справедливо равенство
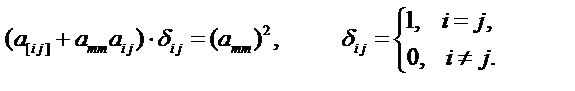
Решение. Предварительно определим следующие тензоры нулевого ранга
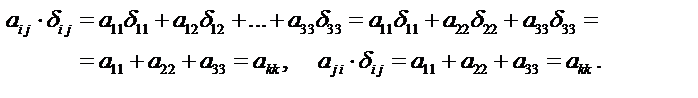
Тогда получим
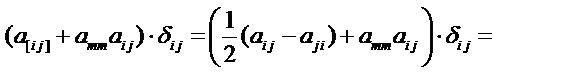
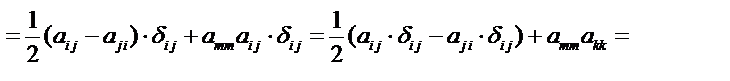
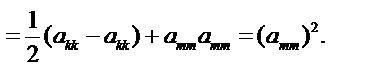
Задача 3. Докажите, что для любого тензора третьего ранга Сijk справедливо равенство
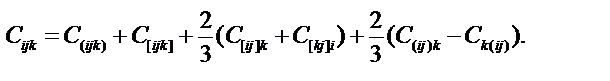
Задача 4. Определите компоненты тензора третьего ранга C [ijk], если известно, что
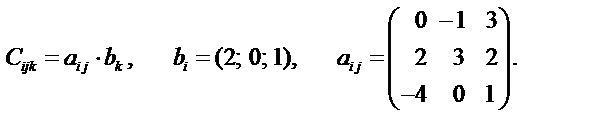
 2015-04-12
2015-04-12 2306
2306
