Тема VI. Элементы векторного анализа

(дифференциальные операции градиент, дивергенция и ротор
в декартовых координатах)

Рассмотрим декартову прямоугольную систему координат с ортонорми­рованным базисом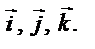

Пусть в некоторой области трехмерного евклидова пространства заданы дважды непрерывно дифференцируемое скалярное поле u(M) и векторное поле 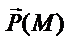. Тогда grad u и 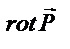образуют векторные поля, а 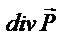образует скалярное поле. В этом случае возможны пять повторных операций:

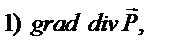
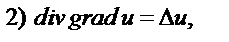
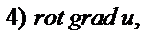
где

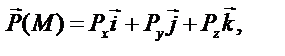
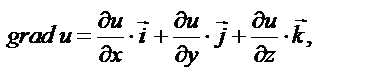
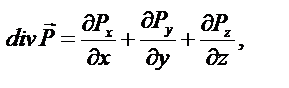
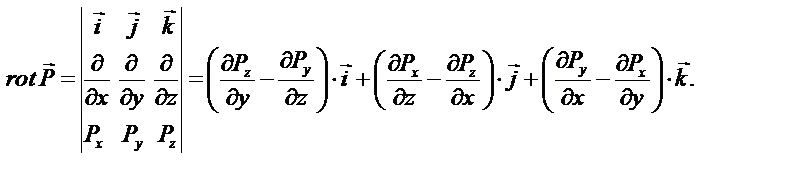
Раскроем повторные операции в общем виде, используя представленные определения.

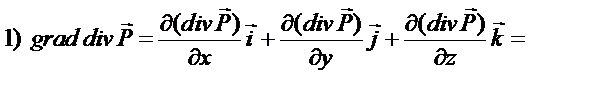
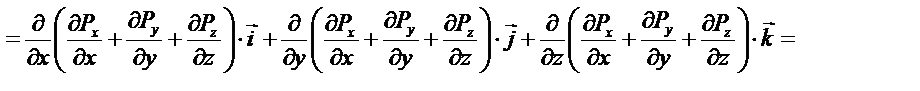
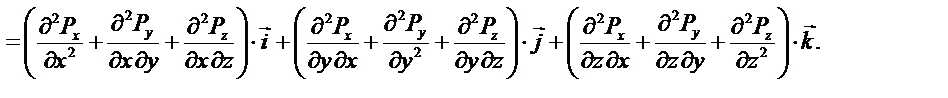
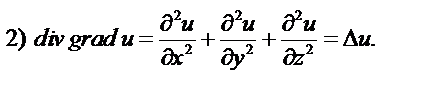
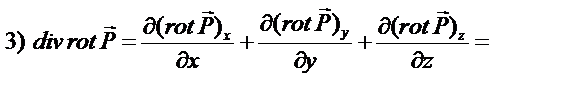
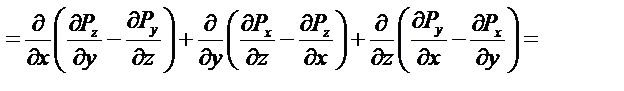
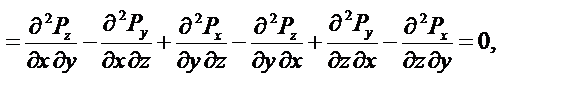
так как смешенные производные не зависят от порядка дифференци­рования.

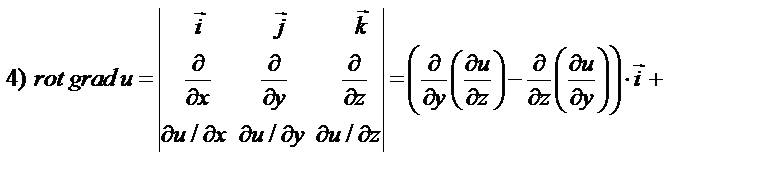
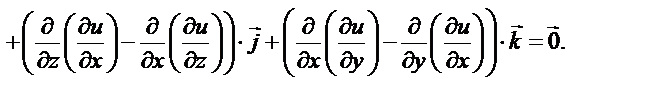
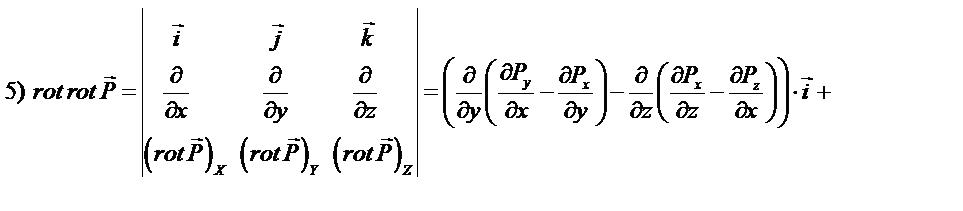
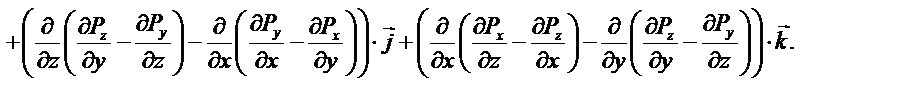
Задача 1. Известно дифференцируемое скалярное поле

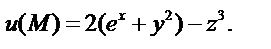
Найдите: 1) grad u, 2) div grad u.

Решение.

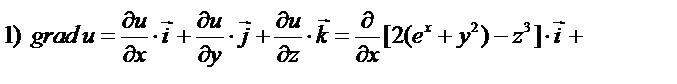
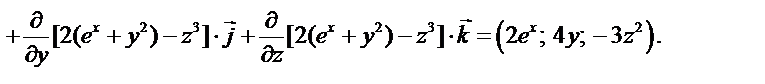
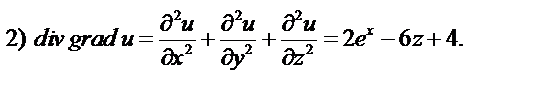
Задача 2. Известны дифференцируемые векторные поля

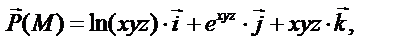
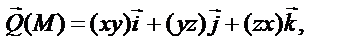
и скалярное поле φ

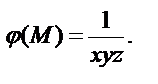
Найдите:

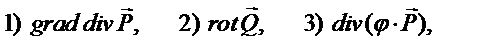
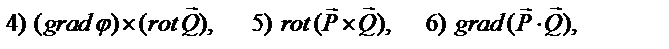
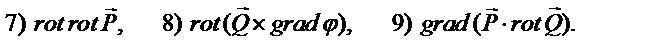
Используйте определение скалярного и векторного произведений

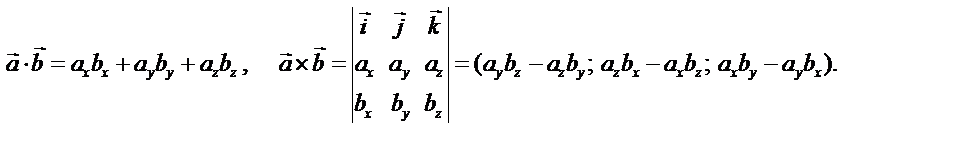
Задачи для домашней контрольной работы

ВАРИАНТ 1(контрольное задание к зачету)

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 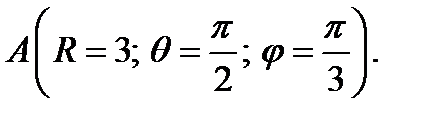Сделайте рисунок локального базиса.

2. Даны тензоры первого ранга b _i = (1; 2; 3) и d _i = (–2; 3; –1). Определите:

1.1. e_[ij]k×b _i ×d_k 1.2. f_ks = b_k×d_s

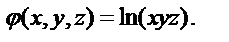3. Дано векторное поле 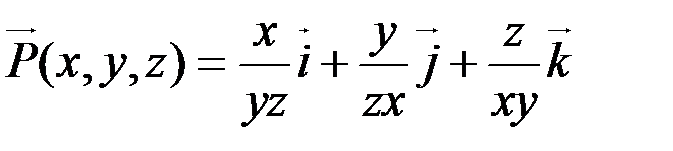и скалярное поле

Определите

ВАРИАНТ 2

1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 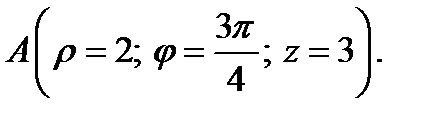Сделайте рисунок локального базиса.

2. Докажите, что для произвольного вектора 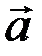выполняется равенство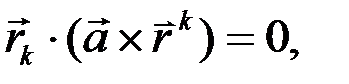

если 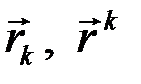– локальный и взаимный базисы криволинейной системы координат.

3. Составьте выражение 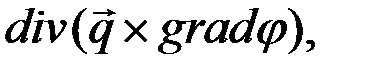если известно, что

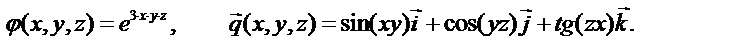
ВАРИАНТ 3

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 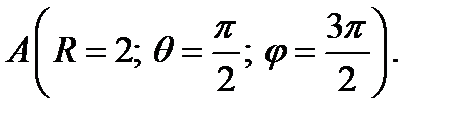Сделайте рисунок локального базиса.

2. Составьте выражение d_[ij] × x_j + d_(ij) × y_j, если известно, что

x_i = (1; -3; 2); y_i = (-2; 1; 2) и d_ij = x_i × y_j

3. По заданному векторному полю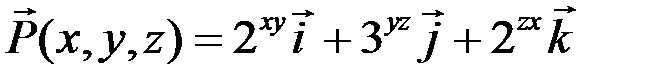

составьте выражение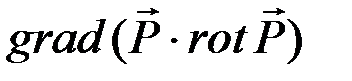

ВАРИАНТ 4

1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 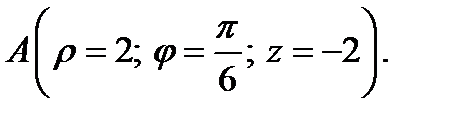Сделайте рисунок локального базиса.

2. Определить компоненты тензорных выражений 1.1. a _[ij]× b ^(ij) 1.2. a _mn× b ^ns

если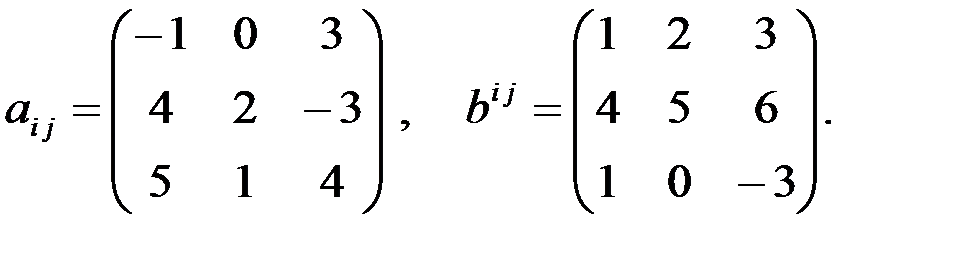

3. Показать, что 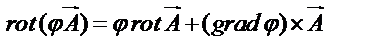и составить выражение для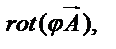

если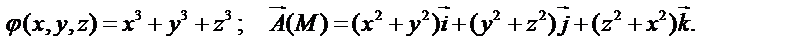

ВАРИАНТ 5

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 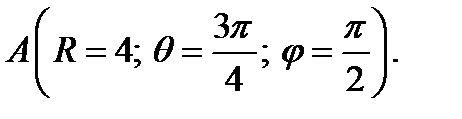Сделайте рисунок локального базиса.

2. Определить компоненты тензора d_[ij] × a_j + d_(ij) × b_j, если известно, что

a_i = (1; 3; –2); b_i = (–2; 1; 2) и d_ij = a_i × b_j

3. Составить выражение 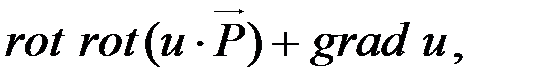если

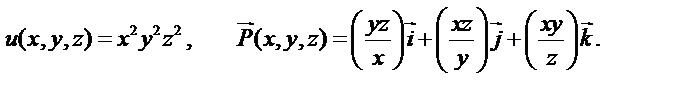
ВАРИАНТ 6

1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 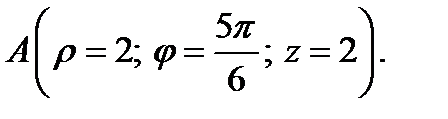Сделайте рисунок локального базиса.

2. Определить компоненты тензоров 1.1. d^ij d_(ij) 1.2. e_ijk d_[ij], если

d_ij = x _i× y _j x _i = (–1; 2; 4) y _i = (3; 2; –3).

3. Составить выражения 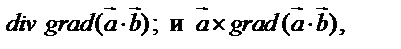если известно, что

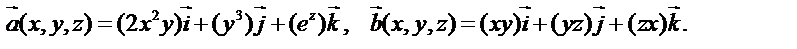
ВАРИАНТ 7

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 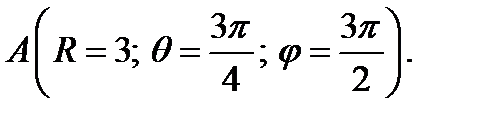Сделайте рисунок локального базиса.

2. В декартовой системе координат задан вектор 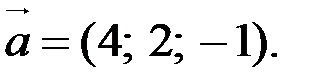Найдите его ковариантные и контравариантные компоненты в точке М(3; p/2; 2) цилиндрической системы координат.

3. Показать, что 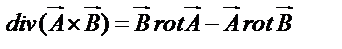и составить выражение для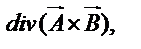

если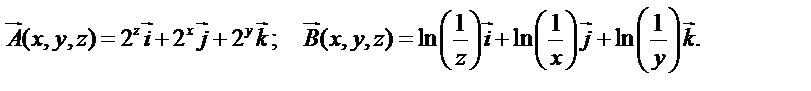

ВАРИАНТ 8

1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 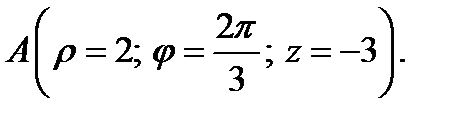Сделайте рисунок локального базиса.

2. Определите компоненты тензорных выражений 1.1. d_(ij) xⁱy^j 1.2. d_ij d ^ij 1.3. d_[ij] xⁱ

Если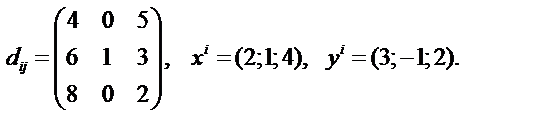

3. По заданным векторным полям

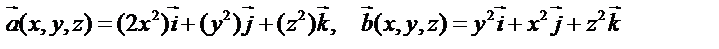
составить выражение для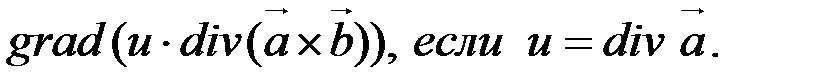

ВАРИАНТ 9

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 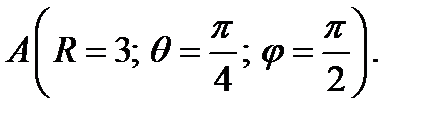Сделайте рисунок локального базиса.

2.Докажите, что выполняется равенство 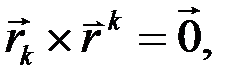если 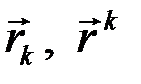– локальный и взаимный базисы криволинейной системы координат.

3. Покажите, что для любой функции j(x, y, z) справедливо равенство
rot (j× grad j) = 0 и составьте выражение Div (j× grad j), если

j(x, y, z) = sin(x y z).

ВАРИАНТ 10

1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 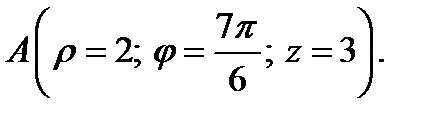Сделайте рисунок локального базиса.

2. Разложите тензор 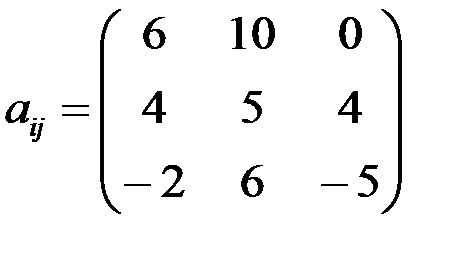на симметричный (b_ij) и кососимметричный (d_ij) и найдите 2.1. a_ij×b_ij 2.2. a_ss(b_ij – d_ij) 2.3. (b_rr×d_ij + b_ij)a_ij

3. Составить выражение 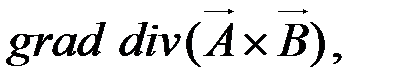если

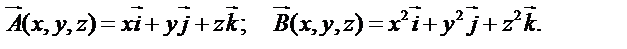
ВАРИАНТ 11

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 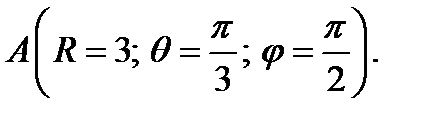Сделайте рисунок локального базиса.

2. В декартовой системе координат задан вектор 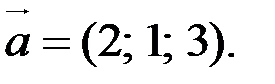Найдите его ковариантные и контравариантные компоненты в точке А(3; p/2; p/2) сферической системы координат.

3. Показать, что 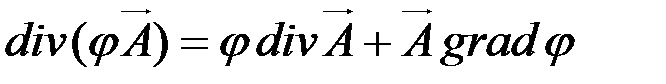и составить выражение для

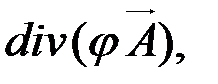если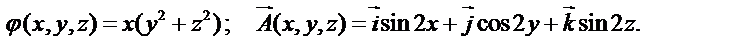

ВАРИАНТ 12

1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 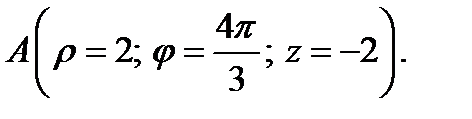Сделайте рисунок локального базиса.

2. Определите компоненты тензорных выражений 1.1. d_(ij) xⁱy^j 1.2. d_ij d ^ij 1.3. d_[ij] xⁱ

Если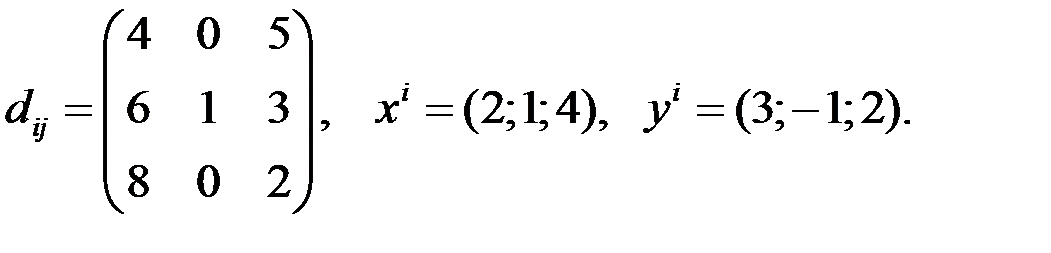

3. По заданным векторным полям

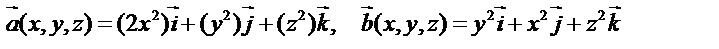
составить выражение для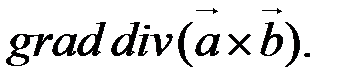

ВАРИАНТ 13

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 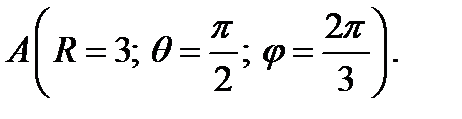Сделайте рисунок локального базиса.

2. Даны тензоры первого ранга b _i = (3; 2; 1) и d _i = (–2; 3; –1). Определите:

1.1. e_i[jk]×b _i ×d_k 1.2. f_ks = b_k×d_s

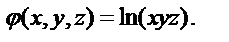3. Дано векторное поле 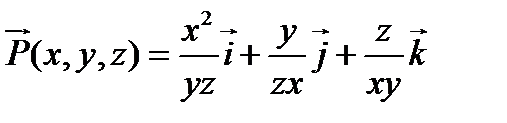и скалярное поле

Определите

ВАРИАНТ 14

1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 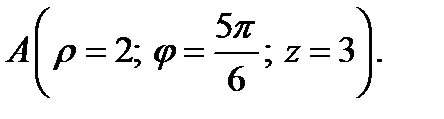Сделайте рисунок локального базиса.

2. Докажите, что для произвольного вектора 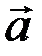выполняется равенство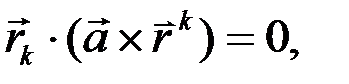

если 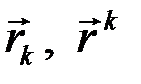– локальный и взаимный базисы криволинейной системы координат.

3. Составьте выражение 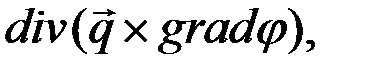если известно, что

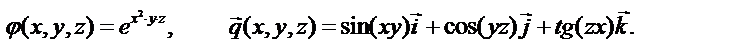
ВАРИАНТ 15

1. Определите векторы локального и взаимного базисов сферической системы координат в точке 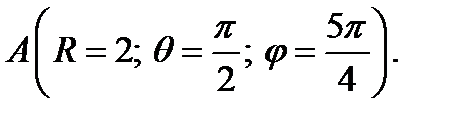Сделайте рисунок локального базиса.

2. Составьте выражение d_[ij] × x_j + d_(ij) × y_j, если известно, что

x_i = (1; -3; 2); y_i = (-2; 1; 2) и d_ij = x_i × y_j

3. По заданному векторному полю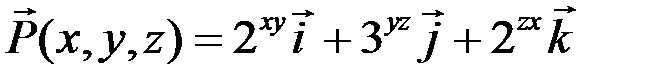

составьте выражение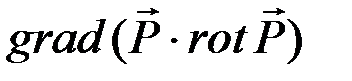

ВОПРОСЫ К ЗАЧЕТУ

ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА

1. Локальный базис криволинейной системы координат.
2. Взаимный базис. Ковариантные и контравариантные проекции вектора.
3. Преобразование координат, базиса и компонент вектора.
4. Определение тензора.
5. Декартовы тензоры.
6. Операции тензорной алгебры. Сложение и произведение тензоров.
7. Операции тензорной алгебры. Перестановка индексов, свертка тензора.
8. Операции тензорной алгебры. Симметрирование тензора.
9. Операции тензорной алгебры. Альтернирование тензора.
10. Смешанный тензор второго ранга, как линейный оператор.
11. Матрица линейного оператора.
12. Инварианты линейного оператора.
13. Дивергенция и ротор линейного оператора.
14. Дивергенция и ротор линейного оператора в ортонормированном базисе.
15. Дифференцируемое скалярное поле. Градиент скалярного поля.
16. Производная скалярного поля по направлению.
17. Дифференцируемое векторное поле. Дивергенция и ротор векторного поля.
18. Производная векторного поля по направлению.
19. Производная векторного поля по направлению в ортонормированном базисе.
20. Повторные операции теории поля.
21. Символическая запись операций теории поля.
22. Градиент скалярного поля в криволинейных координатах.
23. Дивергенция векторного поля в криволинейных координатах.
24. Ротор векторного поля в криволинейных координатах.
25. Теорема Остроградского, теорема Грина, теорема Стокса.