1. Дифференциальные уравнения первого порядка. Теорема Коши. Задача Коши. Общее и частное решение, интегральная кривая.
2. Уравнения с разделяющимися переменными.
3. Решение уравнений вида 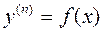 .
.
4. Линейные однородные дифференциальные уравнения. Теорема об общем решении однородного уравнения. Фундаментальная система решений. Определитель Вронского.
5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение.
6. Общее решение линейных однородных дифференциальных уравнений с постоянными коэффициентами второго порядка при условии, что характеристическое уравнение имеет два различных действительных корня.
7. Общее решение линейных однородных дифференциальных уравнений с постоянными коэффициентами второго порядка при условии, что характеристическое уравнение имеет кратный корень.
8. Общее решение линейных однородных дифференциальных уравнений с постоянными коэффициентами второго порядка при условии, что характеристическое уравнение имеет комплексные корни.
9. Общее решение линейных однородных дифференциальных уравнений с постоянными коэффициентами высшего порядка (n >2).
10. Линейные дифференциальные уравнения. Теорема об общем решении неоднородного уравнения. Теорема наложения.
11. Нахождение частного решения линейного неоднородного дифференциального уравнения при условии, что правая часть имеет вид 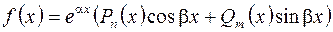 .
.
12. Нахождение частного решения линейного неоднородного дифференциального уравнения при условии, что правая часть – многочлен n степени.
13. Нахождение частного решения линейного неоднородного дифференциального уравнения при условии, что правая часть имеет вид 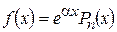 .
.
14. Нахождение частного решения линейного неоднородного дифференциального уравнения при условии, что правая часть имеет вид 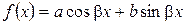 .
.
15. Системы дифференциальных уравнении. Сведение системы двух дифференциальных уравнений к одному уравнению второго порядка.
Ряды.
1. Числовые ряды. Геометрическая прогрессия. Необходимый признак сходимости. Свойства сходящихся рядов.
2. Ряды с неотрицательными членами. Признаки сравнения. Признаки Даламбера и Коши. Интегральный признак.
3. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды. Признак Лейбница.
4. Функциональные и степенные ряды. Ряды Маклорена и Тейлора. Разложение функций в степенные ряды и их применение.
Задачи
1. Построить линии уровня функции 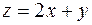 .
.
2. Построить линии уровня функции 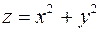 .
.
3. Построить линии уровня функции 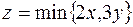 .
.
4. Построить линии уровня функции 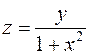 .
.
5. Построить линии уровня функции 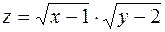 .
.
6. Построить линии уровня и градиент функции 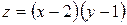 в точке (1,1).
в точке (1,1).
7. Посчитать частные производные функции второго порядка функции 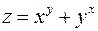 .
.
8. Посчитать частные производные первого порядка функции 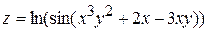
9. Найти производную функции, заданной неявно 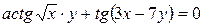
10. Найти точки экстремума функций
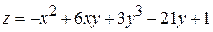
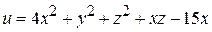
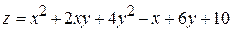 .
.
11. Найти экстремум функции 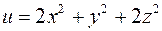 при условии
при условии 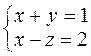 .
.
12. Найти экстремум функции 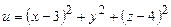 при условии
при условии 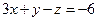
13. Найти экстремум функции 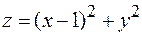 при условии
при условии 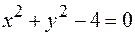 . Решить задачу с помощью функции Лагранжа. Дать графическую интерпретацию полученного решения.
. Решить задачу с помощью функции Лагранжа. Дать графическую интерпретацию полученного решения.
14. Найти экстремум функции 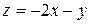 при условии
при условии
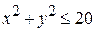
Изобразить на плоскости условие и линии уровня функции в точках экстремума..
15. Производственная функция фирмы 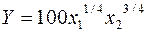 . Цены ресурсов
. Цены ресурсов 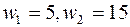 . Найти наибольший выпуск продукции и спрос на ресурсы
. Найти наибольший выпуск продукции и спрос на ресурсы 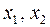 при издержках
при издержках 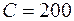 .
.
16. Производственная функция фирмы 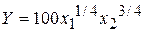 . Цены ресурсов
. Цены ресурсов 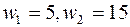 . Фирма должна по договору обеспечить поставку 1000 ед. продукции. Найти минимальные издержки фирмы и спрос на ресурсы
. Фирма должна по договору обеспечить поставку 1000 ед. продукции. Найти минимальные издержки фирмы и спрос на ресурсы 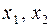 .
.
17. 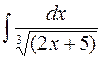 .
.
18. 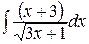
19. 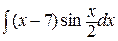 .
.
20. 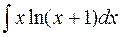 .
.
21. 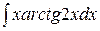
22. 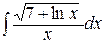 .
.
23. 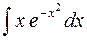 .
.
24. 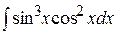 .
.
25. 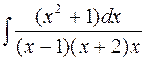 .
.
26. 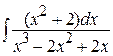
27. 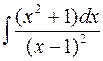 .
.
28. 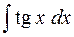 .
.
29. 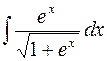 .
.
30. 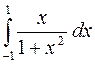 .
.
31. 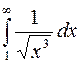 .
.
32. 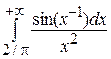
33. 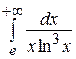 .
.
34. 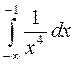 .
.
35. 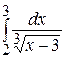
36. 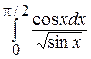
37. 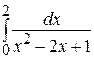
38. Найти корни уравнения 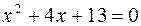 в комплексных числах и найти их сумму и произведение.
в комплексных числах и найти их сумму и произведение.
39. Найти решение уравнения 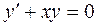 , удовлетворяющее условию
, удовлетворяющее условию 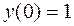 .
.
40. 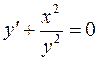 .
.
41. 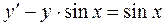 .
.
42. 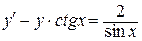
43. 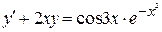
44. 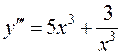 .
.
45. Найти решение уравнения 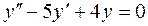 , удовлетворяющее условиям
, удовлетворяющее условиям 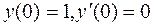 .
.
46. 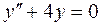 .
.
47. Найти решение уравнения 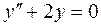 , удовлетворяющее условиям
, удовлетворяющее условиям 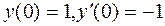 .
.
48. 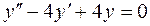 .
.
49. 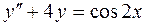 .
.
50. 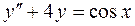 .
.
51. 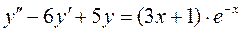 .
.
52. 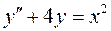 .
.
53. 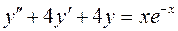 .
.
54. 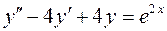 .
.
55. 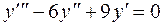 .
.
56. 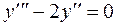 .
.
57. 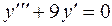 .
.
58. 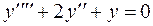 .
.
59. 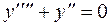 .
.
60. Решить систему уравнений сведением к одному уравнению второго порядка
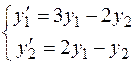 .
.
61. Исследуйте сходимость рядов:
а) 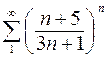 , б)
, б) 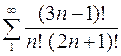 , в)
, в) 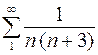 , г)
, г) 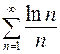 , д)
, д) 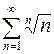 .
.
62. Исследовать ряды на абсолютную и условную сходимость:
а) 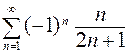 , б)
, б) 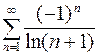 , в)
, в) 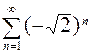 , г)
, г) 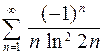 .
.
63. Найдите области сходимости функциональных рядов: а) 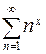 , б)
, б) 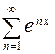 .
.
64. Найдите промежутки сходимости степенных рядов:
а) 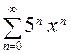 , б)
, б) 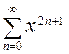 , в)
, в) 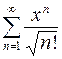 , г)
, г) 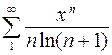 , д)
, д) 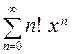 .
.
65. Разложите в ряд Маклорена функции:
а) 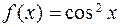 , б)
, б) 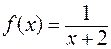 , в)
, в) 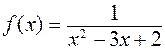 .
.
66. Найдите приближенное значение интеграла 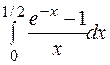 , оцените погрешность.
, оцените погрешность.
67. Решите задачу Коши с помощью степенного ряда 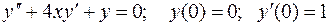 .
.
 2015-04-20
2015-04-20 424
424








