Поскольку электромагнитные колебания в линии распространяются с конечной скоростью, не превышающей скорости распространения света, то мгновенные значения напряжения u и тока i в любой точке линии являются не только функциями времени t, но и расстояния от начала линии x: u(x,t); i(x,t). В элементах с сосредоточенными параметрами ток и напряжение зависят только от времени t: u(t), i(t).
Для элемента линии длиной dx на основании законов Кирхгофа, пренебрегая величинами второго порядка малости, можно записать уравнения:
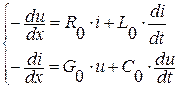 (2.1)
(2.1)
Данные уравнения называются телеграфными, поскольку впервые были получены для телеграфной связи. Решение телеграфных уравнений в общем виде – задача сложная, поэтому рассмотрим частный случай – установившийся режим в линии при воздействии гармонического напряжения на её входе. Если на входе линии действует источник гармонического напряжения
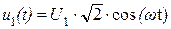 ,
,
то напряжение и ток в любой точке линии с координатой x будут изменяться во времени также по гармоническому закону с частотой входного сигнала ω. Комплексные мгновенные значения напряжения и тока можно записать в виде:
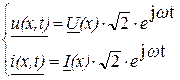 ,
,
где 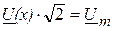 - комплексная амплитуда напряжения;
- комплексная амплитуда напряжения;
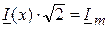 - комплексная амплитуда тока.
- комплексная амплитуда тока.
Подставляя эти выражения в уравнения (2.1), получим систему телеграфных уравнений для комплексных действующих значений:
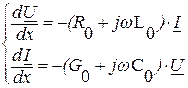 , (2.2)
, (2.2)
где оператору дифференцирования во временной области 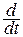 соответствует оператор jω в области комплексной переменной. Продифференцируем уравнения (2.2) по x:
соответствует оператор jω в области комплексной переменной. Продифференцируем уравнения (2.2) по x:
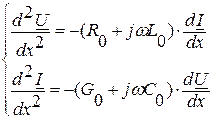 .
.
Подставив в эти выражения значения производных (2.2), получим:
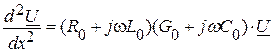 (2.3)
(2.3)
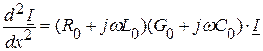 (2.4)
(2.4)
Решение дифференциального уравнения (2.3) имеет вид:
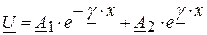 , (2.5)
, (2.5)
где 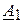 и
и 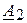 - постоянные интегрирования, а величина
- постоянные интегрирования, а величина
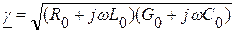 (2.6)
(2.6)
является корнем характеристического уравнения. Эта величина γ называется постоянной распространения, поскольку определяет изменение амплитуды и фазы распространяющегося по линии сигнала.
Аналогичный вид имеет решение уравнения (2.4), однако, чтобы избежать увеличения количества неизвестных постоянных дифференцирования, удобнее определить выражение комплексного действующего значения тока на основании уравнения (2.2):
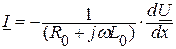 .
.
Согласно (2.5):
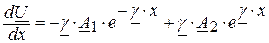 ,
,
тогда
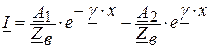 , (2.7)
, (2.7)
где
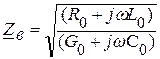 (2.8)
(2.8)
Для того чтобы определить постоянные интегрирования 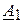 и
и 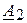 , необходимо ввести дополнительные условия, учитывающие физические процессы в линии. Рассмотрим линию длиной
, необходимо ввести дополнительные условия, учитывающие физические процессы в линии. Рассмотрим линию длиной 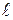 с сопротивлением нагрузки Z н. Тогда комплексные действующие значения напряжения и тока в конце линии можно представить в виде:
с сопротивлением нагрузки Z н. Тогда комплексные действующие значения напряжения и тока в конце линии можно представить в виде:
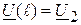 ;
; 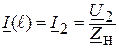 .
.
Применив эти условия к (2.5) и (2.7), получим:
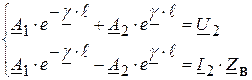 .
.
Из решения этой системы уравнений находим постоянные интегрирования:
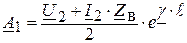 ,
, 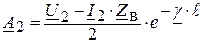 .
.
Подставляя значения 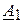 и
и 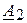 в (2.5) и (2.7), получим формулы для расчёта комплексных значений напряжения и тока в любой точке линии:
в (2.5) и (2.7), получим формулы для расчёта комплексных значений напряжения и тока в любой точке линии:
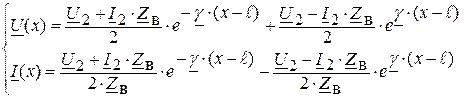 (2.9)
(2.9)
Вместо координаты x, отсчитываемой от начала линии, в ряде случаев удобно использовать координату 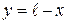 , отсчитываемую от конца линии. В этом случае уравнения (2.9) приобретают вид:
, отсчитываемую от конца линии. В этом случае уравнения (2.9) приобретают вид:
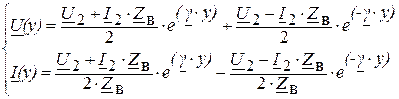 (2.10 а)
(2.10 а)
Можно сгруппировать слагаемые, входящие в уравнения (2.10 а), иначе:
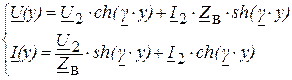 (2.10 б)
(2.10 б)
Если в качестве дополнительных условий, учитывающих физические процессы в линии, ввести комплексные действующие значения напряжения и тока в начале линии 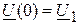 ;
; 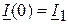 , то формулы для расчёта комплексных значений напряжения и тока в любой точке линии:
, то формулы для расчёта комплексных значений напряжения и тока в любой точке линии:
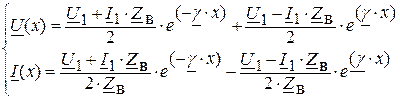 (2.11)
(2.11)
Уравнения (2.9), (2.10) и (2.11) называются уравнениями передачи однородной длинной линии.
 2015-03-22
2015-03-22 1478
1478
