Формулы называют равносильными, если при любых подстановках предметных постоянных они принимают одинаковое значение. Если две формулы F 1 и F 2 равносильны, т. е. F 1º F 2, то они эквивалентны.
Если формула алгебры предикатов F имеет вхождением подформулу Fi, т. е. F (t 1, t 2,¼, Fi, ¼), для которой существует эквивалентная ей подформула Fj т.е. Fi = Fj, то возможна подстановка всюду в формулу F вместо формулы Fi подформулу Fj без нарушения истинности формулы, т.е.
F (t 1, t 2,¼, Fi, ¼)º F (t 1, t 2,¼, Fj, ¼).
Если в законах алгебры высказываний вместо имеющихся пропозициональных переменных всюду подставить предикаты так, чтобы вместо одной и той же пропозициональной переменной стоял один и тот же предикат, то получится закон алгбры предикатов.
Основные законы эквивалентных преобразований алгебры предикатов представлены в табл. 1.
Таблица 1
| Наименование закона и правила | Равносильные формулы Fi º Fj |
| коммутативности | " x " y (F 2(x, y)) º" y " x (F 2(x, y))*); $ x $ y (F 2(x, y)) º$ y $ x (F 2(x, y))*). *) только для одноименным кванторов. |
| дистрибутивности | " x (F 1(x))Ù" x (F 2(x)) º" x (F 1(x)Ù F 2(x))*); $ x (F 1(x))Ú$ x (F 2(x)) º$ x (F 1(x)Ú F 2(x))**); *)для логической связки Ù формул только с кванторами " по одной переменной x. **)для логической связки Ú формул только с кванторами $ по одной переменной x. |
| идемпотентности ÂÎ{";$} | Â x (F (x))Ú Â x (F (x)) º Â x (F (x)); Â x (F (x))ÙÂ x (F (x)) º Â x (F (x)) |
| исключенного третьего | Â x (F (x))Ú 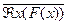 º1, где ÂÎ{";$} º1, где ÂÎ{";$} |
| противоречия | Â x (F (x))Ù 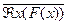 º0, где ÂÎ{";$} º0, где ÂÎ{";$} |
| де Моргана | " x (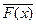 ) º ) º 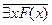 ; $ x ( ; $ x (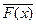 ) º ) º 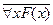 |
| двойного отрицания | 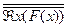 ºÂ x (F (x)), где ÂÎ{";$} ºÂ x (F (x)), где ÂÎ{";$} |
| свойства констант |  x (F (x))Ú0ºÂ x (F (x));  x (F (x))Ú1º1;  x (F (x))Ù0º0;  x (F (x))Ù1ºÂ x (F (x)), где ÂÎ{";$}. |
Пример. Упростить формулу
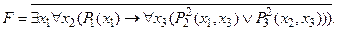
1) Выполнить операцию отрицания формулы:
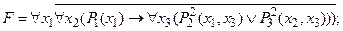
2) выполнить операцию отрицания формулы:
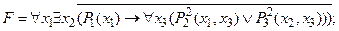
3) удалить логическую связку ®:
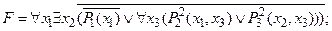
4) выполнить операцию отрицания формулы:
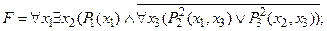
5) выполнить операцию отрицания формулы:
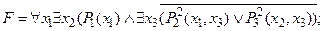
6) выполнить операцию отрицания формулы:
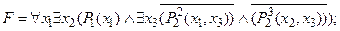
7) перенести квантор $ x 3 влево:
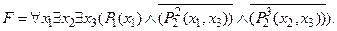
Пример. Упростить формулу
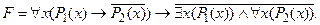
1) Удалить логическую связку ®:
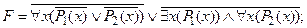
2) выполнить операцию отрицания формулы:
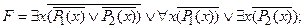
3) выполнить операцию отрицания формулы:
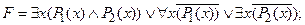
4) применить закон дистрибутивности по квантору $ x:
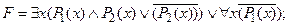
5) применить закон дистрибутивности к формуле:
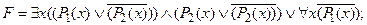
6) применить закон исключенного третьего и свойство констант для логической связки Ù:
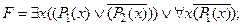
7) применить закон де Моргана:
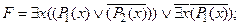
8) применить закон дистрибутивности по квантору $ x:
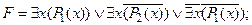
9) применить закон исключенного третьего:
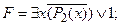
3) применить свойство констант для логической связки Ú: F =1, т. е. формула
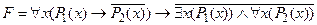
является тождественно истиной.
 2015-04-12
2015-04-12 952
952








