Шаг 1. Исключить всюду логические операции ® и «по правилам:
F 1® F 2º 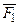 Ú F 2;
Ú F 2;
(F 1«F 2)=(F 1® F 2)Ù (F 2® F 1)=(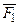 Ú F 2)Ù(
Ú F 2)Ù(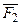 Ú F 1).
Ú F 1).
Шаг 2. Продвинуть отрицание до элементарной формулы по правилам:
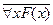 º$ x (
º$ x (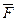 ),
), 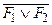 º
º 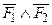 ,
,
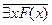 º" x (
º" x (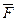 ),
), 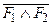 º
º 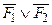 .
.
Шаг 3. Переименовать связанные переменные по правилу: «найти самое левое вхождение предметной переменной такое, что это вхождение связано некоторым квантором, но существует еще одно вхождение этой же переменной; затем сделать замену связанного вхождения на вхождение новой переменной», операцию повторять пока возможна замена связанных переменных;
Шаг 4. Вынести кванторы влево по законам алгебры предикатов.
Шаг 5. Преобразовать бескванторную матрицу к виду КНФ. Алгоритм приведения матрицы формулы к виду КНФ приведен в алгебре высказываний.
Пример. 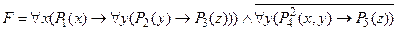 .
.
Привести формулу к виду ПНФ.
l) удалить логические связки ®:
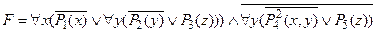 ;
;
2) применить закон де Моргана 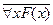 º$ x (
º$ x (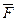 ):
):
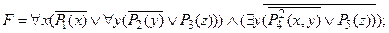
3) применить закон де Моргана 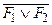 º
º 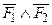 :
:
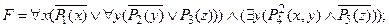
4) переименовать связанную переменную x = w:
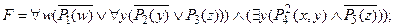
5) переименовать связанную переменную y = v:
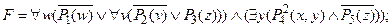
6) вынести квантор " v влево:
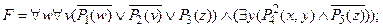
7) вынести квантор $ y влево:
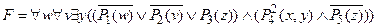 .
.
Матрица ПНФ содержит три элементарных дизъюнкта:
S ={ 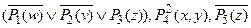 }.
}.
Пример. 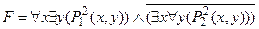 .
.
Привести формулу к виду ПНФ.
1) применить закон 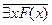 º" x (
º" x (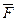 ):
):
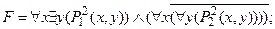
2) применить закон 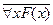 º$ x (
º$ x (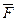 ):
):
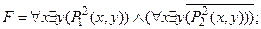
8) вынести квантор " x по закону дистрибутивности:
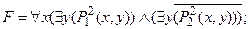
4) переименовать связанную переменную y = z:
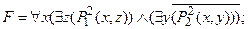
5) вынести кванторы $ z и $ y влево:
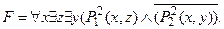
Матрица ПНФ содержит два элементарных дизъюнкта:
S ={ 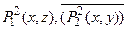 }.
}.
Пример. Привести формулу к виду ПНФ
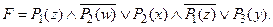
1) по закону дистрибутивности:
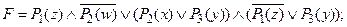
2) по закону дистрибутивности:
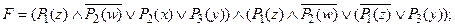
3) по закону дистрибутивности:
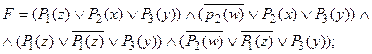
4) по закону исключенного третьего:
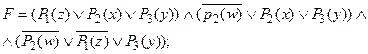
Матрица содержит три элементарных дизъюнкта:
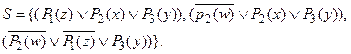
Дизъюнкты матрицы содержат контрарные атомы P 1.(z) и 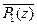 , P 2.(x) и
, P 2.(x) и 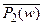 , свободные переменные которых могут быть одинаковыми или разными.
, свободные переменные которых могут быть одинаковыми или разными.
2.2.5. Сколемовская стандартная форма
Наличие разноименных кванторов усложняет вывод заключения. Поэтому рассмотрим класс формул, содержащих только кванторы всеобщности. Формула F называется "–формулой, если она представлена в ПНФ и содержит только кванторы всеобщности, т. е.
F = " x 1 " x 2 ¼ " xn (M).
Для устранения кванторов существования из префикса формулы разработан алгоритм Сколема, вводящий сколемовскую функцию для связывания предметной переменной квантора существования с другими предметными переменными.
 2015-04-12
2015-04-12 5297
5297








