ТЕОРИЯ ПРЕДЕЛОВ
Основные свойства пределов и эквивалентные функции
3.2 Раскрытие неопределенности вида 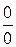
3.3 Раскрытие неопределенности вида 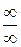
3.4 Раскрытие неопределенности вида 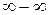
Вычисление пределов от трансцендентных функций
Вычисление предела степенно-показательной функции
Задания для индивидуальной работы
№1
1) 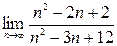 ; 2)
; 2) 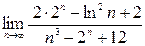 ;3)
;3) 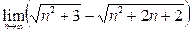
4) 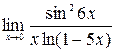 ; 5)
; 5) 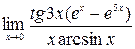 ; 6)
; 6) 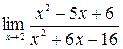 ;
;
7) 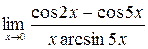 ; 8)
; 8) 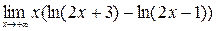 ;
;
9) 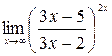 ;10)
;10) 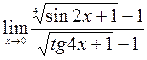
№2
1) 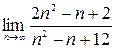 ; 2)
; 2) 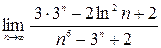 ; 3)
; 3) 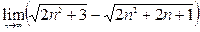 ;4)
;4) 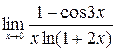 ; 5)
; 5) 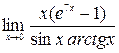 ; 6)
; 6) 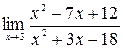 ;
;
7) 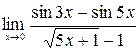 ; 8)
; 8) 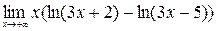 ;
;
9) 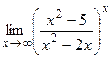 ;10)
;10) 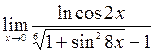
№3
1) 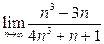 ; 2)
; 2) 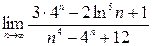 ;3)
;3) 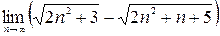 ;
;
4) 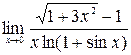 ;5)
;5) 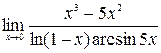 ;6)
;6) 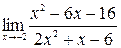 ;
;
7) 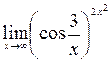 ; 8)
; 8) 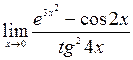 ; 9)
; 9) 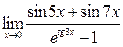 ; 10)
; 10) 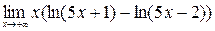 .
.
№4
1) 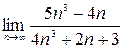 ; 2)
; 2) 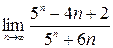 ; 3)
; 3) 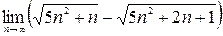
4) 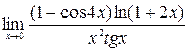 ; 5)
; 5) 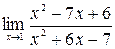 ; 6)
; 6) 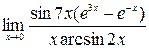 ; 7)
; 7) 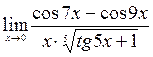 ; 8)
; 8) 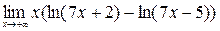 ;
;
9) 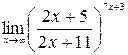 ; 10)
; 10) 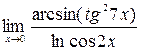
№5
1) 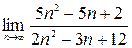 ;2)
;2) 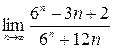 ; 3)
; 3) 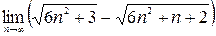 ;
;
4) 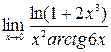 ; 5)
; 5) 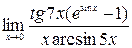 ;6)
;6) 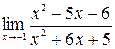 ;
;
7) 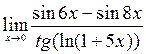 ; 8)
; 8) 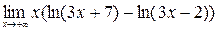 ;
;
9) 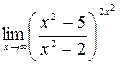 ;10)
;10) 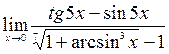 .
.
№6
1) 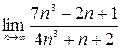 ; 2)
; 2) 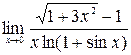 ; 3)
; 3) 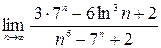 ; 4)
; 4) 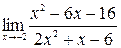 ; 5)
; 5) 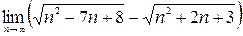 ; 6)
; 6) 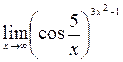 ; 7)
; 7) 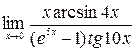 ; 8)
; 8) 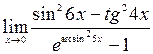 ; 9)
; 9) 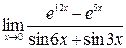 ; 10)
; 10) 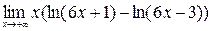 .
.
№7
1) 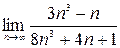 ; 2)
; 2) 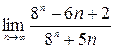 ;3)
;3)  ;
;
4) 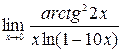 ; 5)
; 5) 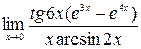 ; 6)
; 6) 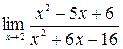 ;
;
7) 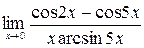 ; 8)
; 8) 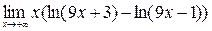 ;
;
9) 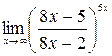 ;10)
;10) 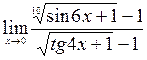
№8
1) 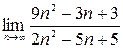 ;2)
;2) 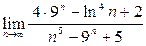 ;3)
;3) 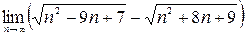 ;
;
4) 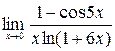 ; 5)
; 5) 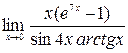 ; 6)
; 6) 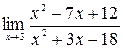 ;7)
;7) 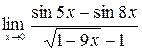 ;
;
8) 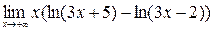 ; 9)
; 9) 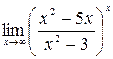 ;10)
;10) 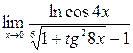
№9
1) 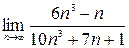 ; 2)
; 2) 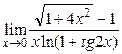 ; 3)
; 3) 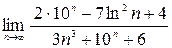 ;
;
4) 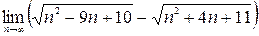 ; 5)
; 5) 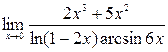 ; 6)
; 6) 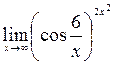 ; 7)
; 7) 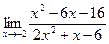 ; 8)
; 8) 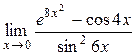 ; 9)
; 9) 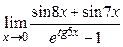 ;
;
10) 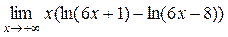 .
.
№10
1) 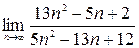 ; 2)
; 2) 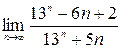 ;3)
;3) 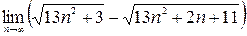 ; 4)
; 4) 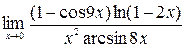 ;5)
;5) 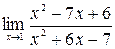 ; 6)
; 6) 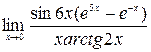 ; 7)
; 7) 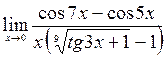 ;8)
;8) 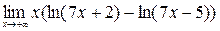 ;
;
9) 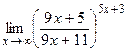 ; 10)
; 10) 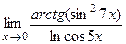 .
.
№11
1) 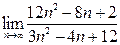 ; 2)
; 2) 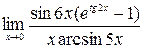 ; 3)
; 3) 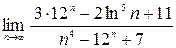 ;
;
4) 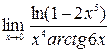 ; 5)
; 5) 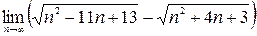 ; 6)
; 6) 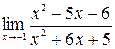 ;
;
7) 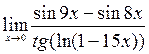 ; 8)
; 8) 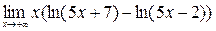 ;
;
9) 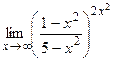 ; 10)
; 10) 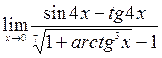 .
.
№12
1) 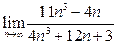 ; 2)
; 2) 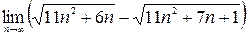 ;
;
3) 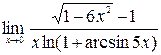 ;4)
;4) 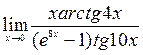 ;5)
;5) 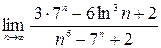 ;
;
6) 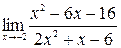 ; 7)
; 7) 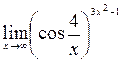 ; 8)
; 8) 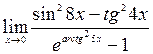 ;
;
9) 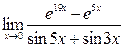 ; 10)
; 10) 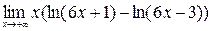
№13
1) 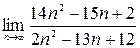 ; 2)
; 2) 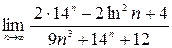 ; 3)
; 3) 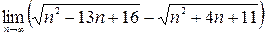 ; 4)
; 4) 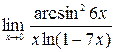 ; 5)
; 5) 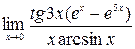 ; 6)
; 6) 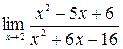 ;7)
;7) 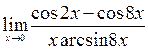 ; 8)
; 8) 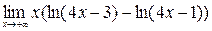 ;
;
9) 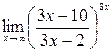 ;10)
;10) 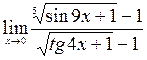 .
.
№14
1) 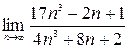 ;2)
;2) 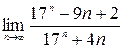 ;3)
;3) 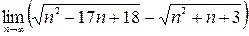 ;
;
4) 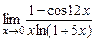 ; 5)
; 5) 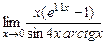 ; 6)
; 6) 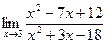 ;7)
;7) 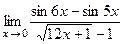 ;
;
8) 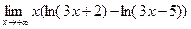 ; 9)
; 9) 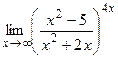 ;10)
;10) 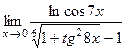
№15
1) 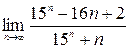 ; 2)
; 2) 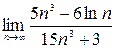 ; 3)
; 3) 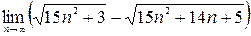
4) 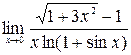 ;5)
;5) 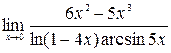 ; 6)
; 6) 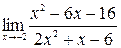 ;
;
7) 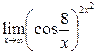 ; 8)
; 8) 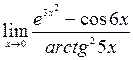 ;
;
9) 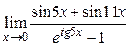 ; 10)
; 10) 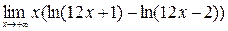 .
.
№16
1) 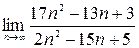 ;2)
;2) 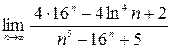 ; 3)
; 3) 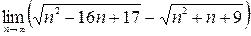 ; 4)
; 4) 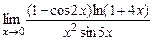 ;5)
;5) 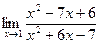 ;
;
6) 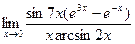 ;7)
;7) 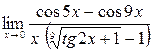 ; 8)
; 8) 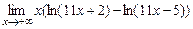
9) 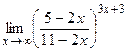 ; 10)
; 10) 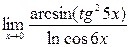 .
.
№17
1) 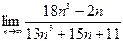 ; 2)
; 2) 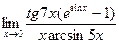 ; 3)
; 3) 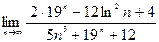 ;
;
4) 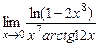 ; 5)
; 5) 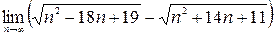 ; 6)
; 6) 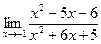 ;
;
7) 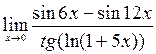 ; 8)
; 8) 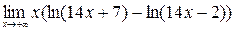 ;
;
9) 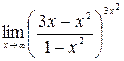 ;10)
;10) 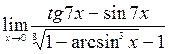 .
.
№18
1) 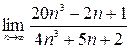 ; 2)
; 2) 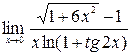 ; 3)
; 3) 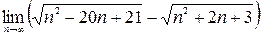
4) 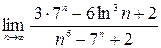 ; 5)
; 5) 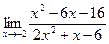 ; 6)
; 6) 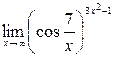 ; 7)
; 7) 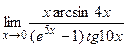 ; 8)
; 8) 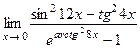 ; 9)
; 9) 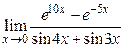
10) 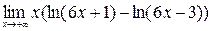 .
.
№19
1) 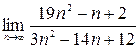 ; 2)
; 2) 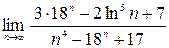 ;
;
3) 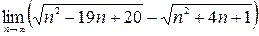 ; 4)
; 4) 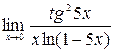 ; 5)
; 5) 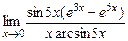 ; 6)
; 6) 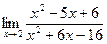 ;7)
;7) 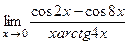 ; 8)
; 8) 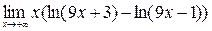 ;
;
9) 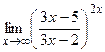 ;10)
;10) 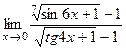 .
.
№20
1) 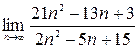 ;2)
;2) 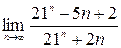 ;
;
3) 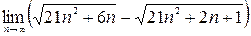 ; 4)
; 4) 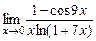 ; 5)
; 5) 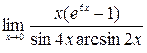 ; 6)
; 6) 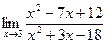 ;7)
;7) 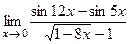 ;8)
;8) 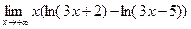
9) 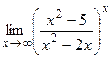 ;10)
;10) 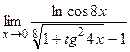 .
.
№21
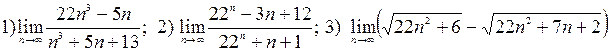 4)
4) 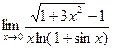 ;5)
;5) 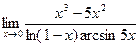 ; 6)
; 6) 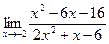 ; 7)
; 7) 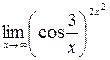 ;
;
8) 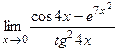 ; 9)
; 9) 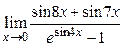 ; 10)
; 10) 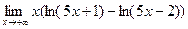
№22
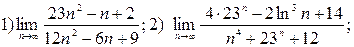
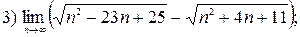 4)
4) 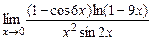 ;
;
5) 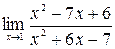 ; 6)
; 6) 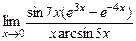 ;7)
;7) 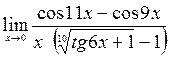 ;
;
8) 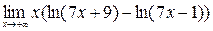 ; 9)
; 9) 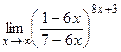 ;10)
;10) 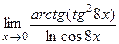 .
.
№23
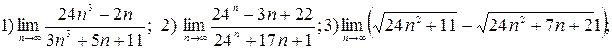
4) 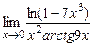 ; 5)
; 5) 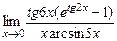 ; 6)
; 6) 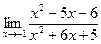 ;
;
7) 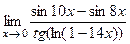 ; 8)
; 8) 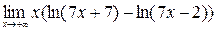 ;
;
9) 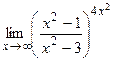 ;10)
;10) 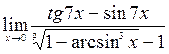 .
.
№24
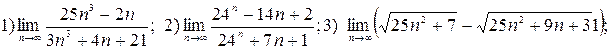 4)
4) 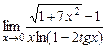 ;5)
;5) 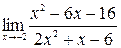 ; 6)
; 6) 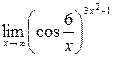 ;
;
7) 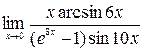 ; 8)
; 8) 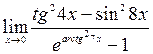 ;
;
9) 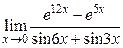 ; 10)
; 10) 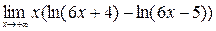 .
.
№25
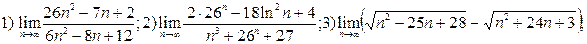
4) 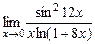 ; 5)
; 5) 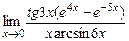 ; 6)
; 6) 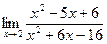 ;7)
;7) 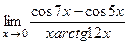 ;
;
8) 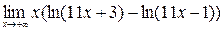 ; 9)
; 9) 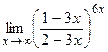 ;10)
;10) 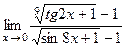 .
.
№26
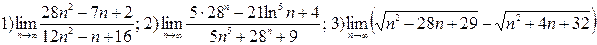 ;
;
4) 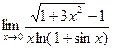 ;5)
;5) 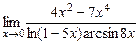 ; 6)
; 6) 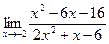 ;
;
7) 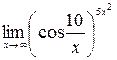 ; 8)
; 8) 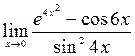 ;
;
9) 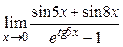 ; 10)
; 10) 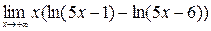 .
.
№27
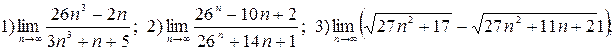 4)
4) 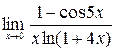 ; 5)
; 5) 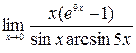 ; 6)
; 6) 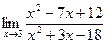 ;
;
7) 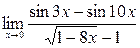 ;8)
;8) 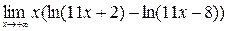 ;
;
9) 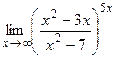 ;10)
;10) 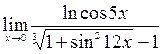 .
.
№28
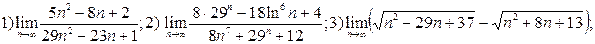 4)
4) 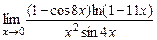 ;5)
;5) 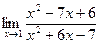 ;6)
;6) 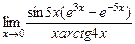 ; 7)
; 7) 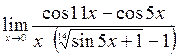 ; 8)
; 8) 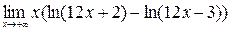 ;
;
9) 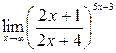 ;10)
;10) 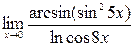 .
.
№29
1) 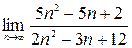 ;2)
;2) 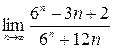 ; 3)
; 3) 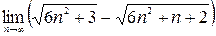 ;
;
4) 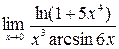 ;5)
;5) 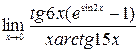 ;6)
;6) 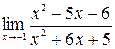 ;
;
7) 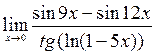 ; 8)
; 8) 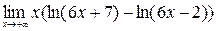 ;
;
9) 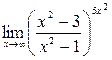 ;10)
;10) 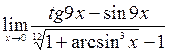 .
.
№30
1) 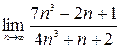 ; 2)
; 2) 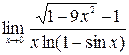 ;3)
;3) 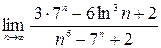 ; 4)
; 4) 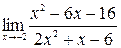 ; 5)
; 5) 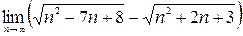 ; 6)
; 6) 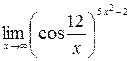 ; 7)
; 7) 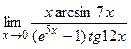 ; 8)
; 8) 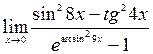 ; 9)
; 9) 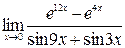 ;10)
;10) 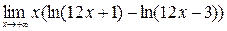 .
.
№31
1) 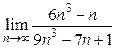 ; 2)
; 2) 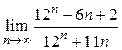 ; 3)
; 3) 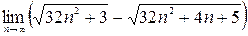
4) 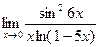 ; 5)
; 5) 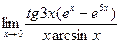 ; 6)
; 6) 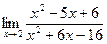 ;
;
7) 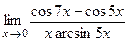 ; 8)
; 8) 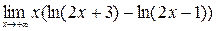 ;
;
9) 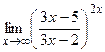 ;10)
;10) 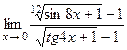 .
.
№32
1) 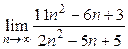 ; 2)
; 2) 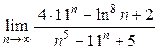 ; 3)
; 3) 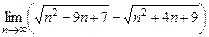
4) 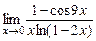 ; 5)
; 5) 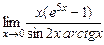 ; 6)
; 6) 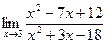 ;7)
;7) 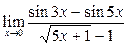 ; 8)
; 8) 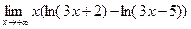 ;9)
;9) 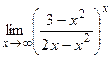 ;10)
;10) 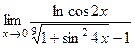 .
.
№33
1) 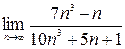 ;2)
;2) 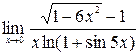 ; 3)
; 3) 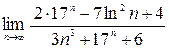 ;
;
3) 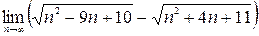 ; 5)
; 5) 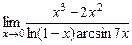 ;
;
6) 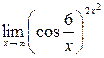 ; 7)
; 7) 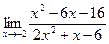 ; 8)
; 8) 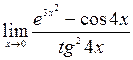 ;
;
9) 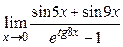 ; 10)
; 10) 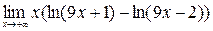 .
.
№34
1) 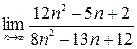 ; 2)
; 2) 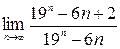 ; 3)
; 3) 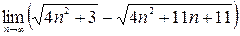 ;
;
4) 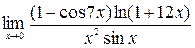 ; 5)
; 5) 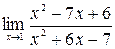 ;6)
;6) 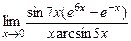 ; 7)
; 7) 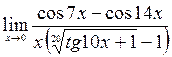 ;8)
;8) 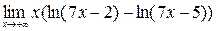 ;
;
9) 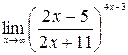 ; 10)
; 10) 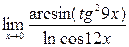 .
.
№35
1) 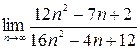 ; 2)
; 2) 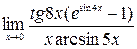 ; 3)
; 3) 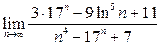 ;
;
4) 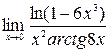 ; 5)
; 5) 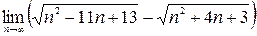 ;
;
6) 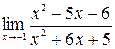 ; 7)
; 7) 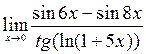 ;8)
;8) 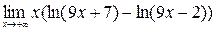 ;
;
9) 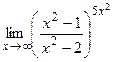 ;10)
;10) 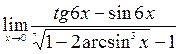 .
.
Глава 4
ПРОИЗВОДНАЯ ФУНКЦИИ
Основные правила дифференцирования
Геометрический смысл производной. Дифференциал функции в точке
Правило Лопиталя
Задания для индивидуальной работы
№1
x5 sin x
(5x+7)5/4
3 cos7x
ctg (5x3)
ln x / e4x-3
Arcsin(tg 3x)
3arctg(ln(2x3-x))
ln4(2ctg3x)+4x
sin(53x+5)-2
 2015-04-12
2015-04-12 639
639







