ü Решить систему уравнений Ax = b, методом Крамера, методом обратной матрицы и методом Гаусса.
1. A= 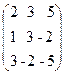 , x =
, x =  , b=
, b= 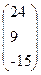 .
.
2. A= 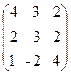 , x =
, x =  , b =
, b = 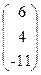 .
.
3. A= 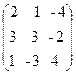 , x =
, x =  , b =
, b = 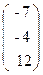 .
.
4. A= 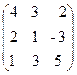 , x =
, x =  , b=
, b= 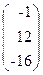 .
.
5. A= 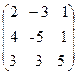 , x =
, x =  , b=
, b= 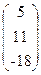 .
.
6. A= 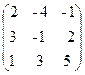 , x =
, x =  , b=
, b= 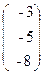 .
.
7. A= 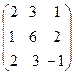 , x =
, x =  , b =
, b = 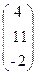 .
.
8. A= 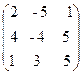 , x =
, x =  , b=
, b= 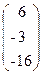 .
.
9. A= 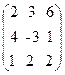 , x =
, x =  , b=
, b= 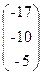 .
.
10. A= 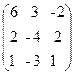 , x =
, x =  , b=
, b= 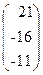 .
.
11. A= 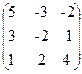 , x =
, x =  , b=
, b= 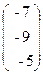 .
.
12. A= 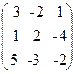 , x =
, x =  , b=
, b= 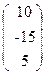 .
.
13. A= 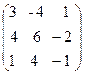 , x =
, x =  , b=
, b= 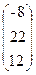 .
.
14. A= 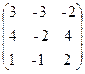 , x =
, x =  , b=
, b= 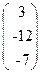 .
.
15. A= 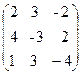 , x =
, x =  , b=
, b= 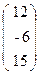 .
.
16. A= 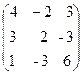 , x =
, x =  , b=
, b= 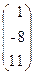 .
.
17. A= 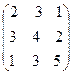 , x =
, x =  , b=
, b= 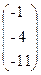 .
.
18. A=  , x =
, x =  , b=
, b= 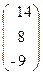 .
.
19. A= 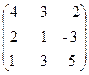 , x =
, x =  , b=
, b= 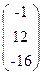
20. A= 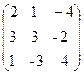 , x =
, x =  , b=
, b= 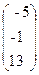 .
.
21. A= 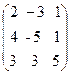 , x =
, x =  , b=
, b= 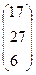 .
.
22. A= 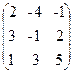 , x =
, x =  , b=
, b= 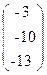 .
.
23. A= 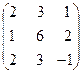 , x =
, x =  , b=
, b= 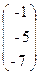 .
.
24. A= 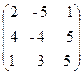 , x =
, x =  , b =
, b = 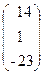 .
.
25. A=  , x =
, x =  , b =
, b = 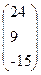 .
.
26. A=  , x =
, x =  , b=
, b= 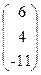 .
.
27. A= 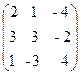 , x =
, x =  , b =
, b = 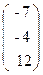 .
.
28. A= 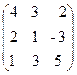 , x =
, x =  , b=
, b= 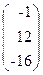 .
.
29. A= 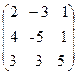 , x =
, x =  , b=
, b= 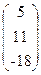 .
.
30. A= 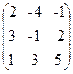 , x =
, x =  , b =
, b = 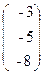 .
.
31. A= 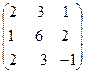 , x =
, x =  , b =
, b = 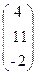 .
.
32. A= 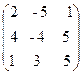 , x =
, x =  , b =
, b = 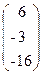 .
.
33. A= 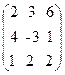 , x =
, x =  , b=
, b= 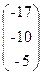 .
.
34. A=  , x =
, x =  , b =
, b = 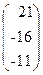 .
.
35. A= 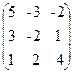 , x =
, x =  , b=
, b= 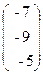 .
.
36. A= 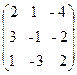 , x =
, x =  , b=
, b= 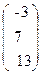 .
.
ü Решить систему уравнений A x = b, методом Гаусса.
37. A= 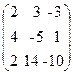 , x=
, x=  , b=
, b= 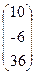 .
.
38. A= 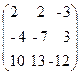 ,x=
,x=  , b=
, b=  .
.
39. A= 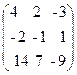 , x=
, x=  , b=
, b= 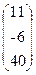 .
.
40. A= 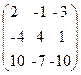 , x=
, x=  , b=
, b= 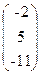 .
.
41. A= 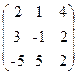 , x=
, x=  , b=
, b= 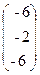 .
.
42. A= 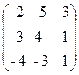 , x=
, x=  , b=
, b= 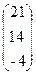 .
.
43. A= 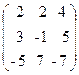 , x=
, x=  , b=
, b= 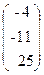 .
.
44. A= 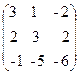 , x=
, x=  , b=
, b= 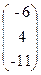 .
.
45. A= 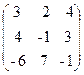 , x=
, x=  , b=
, b=  .
.
46. A= 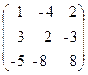 , x=
, x=  , b=
, b= 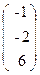 .
.
47. A= 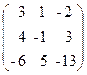 , x=
, x=  ,b=
,b= 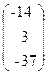 .
.
48. A= 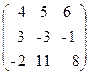 , x=
, x=  ,b=
,b= 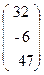 .
.
49. A= 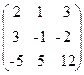 , x=
, x=  , b=
, b= 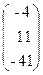 .
.
50. A= 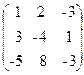 , x=
, x=  , b=
, b= 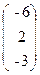 .
.
51. A= 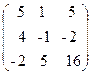 , x=
, x=  , b=
, b= 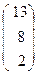 .
.
52. A= 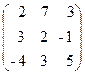 , x=
, x=  , b=
, b= 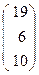 .
.
53. A= 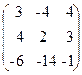 , x=
, x=  , b=
, b= 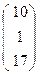 .
.
54. A= 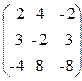 , x=
, x=  , b=
, b= 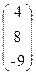 .
.
55. A= 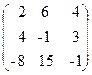 , x=
, x=  , b=
, b= 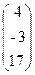 .
.
56. A= 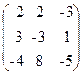 , x=
, x=  , b=
, b= 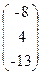 .
.
57. A= 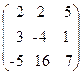 , x=
, x=  , b=
, b= 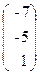 .
.
58. A= 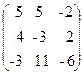 , x=
, x=  , b=
, b= 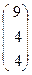 .
.
59. A= 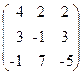 , x=
, x=  , b=
, b= 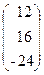 .
.
60. A= 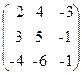 , x=
, x=  , b=
, b= 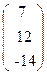 .
.
61. A= 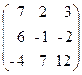 , x=
, x=  , b=
, b= 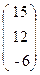 .
.
62. A= 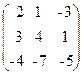 , x=
, x=  , b=
, b= 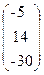 .
.
63. A= 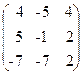 , x=
, x=  , b=
, b= 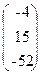 .
.
64. A= 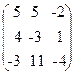 , x=
, x=  , b=
, b= 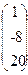 .
.
65. A= 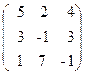 , x=
, x=  , b=
, b= 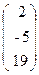 .
.
66. A= 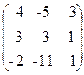 , x=
, x=  , b=
, b= 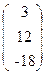 .
.
67. A= 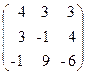 , x=
, x=  , b=
, b= 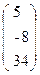 .
.
68. A= 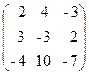 , x=
, x=  , b=
, b=  .
.
69. A= 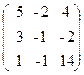 , x=
, x=  , b=
, b= 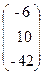 .
.
70. A= 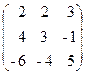 , x=
, x=  , b=
, b= 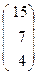 .
.
71. A= 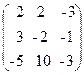 , x=
, x=  , b=
, b= 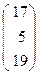 .
.
72. A= 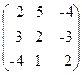 , x=
, x=  , b=
, b= 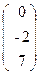 .
.
73. A= 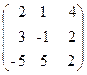 , x=
, x=  , b=
, b= 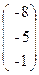 .
.
74. A= 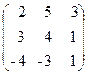 , x=
, x=  , b=
, b= 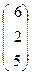 .
.
75. A= 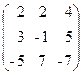 , x=
, x=  , b=
, b=  .
.
76. A= 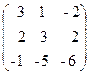 , x=
, x=  , b=
, b= 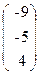 .
.
1.3 Пространство Rn
· Векторы. Пусть 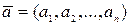 и
и 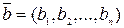 .
.
o Сумма: 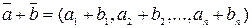 ;
;
o Произведение на число: 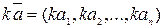 ;
;
o Норма (длина вектора) 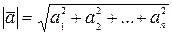 ;
;
o Угол между векторами: 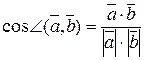 ;
;
o Векторы 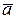 и
и 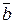 перпендикулярны, если
перпендикулярны, если 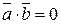 ;
;
o Векторы 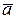 и
и 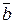 параллельны, если
параллельны, если 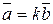 ,
, 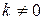 ;
;
o Если A(x1, y1, z1) и B(x2, y2, z2), то 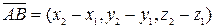 .
.
· Линейная зависимость и линейная независимость системы векторов. Пусть 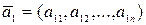 ,
, 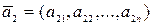 ,…,
,…, 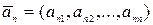 .
.
o Система векторов 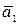 ,
, 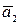 ,…,
,…, 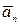 линейна независима
линейна независима 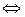
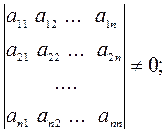
o Система векторов 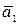 ,
, 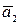 ,…,
,…, 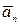 линейна зависима
линейна зависима 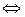
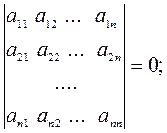
o Векторы 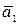 и
и 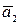 линейно зависимы
линейно зависимы 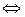
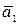 и
и 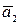 параллельны.
параллельны.
 2015-04-12
2015-04-12 802
802

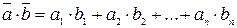 ;
;






