При кручении стержня (рис. 4.1 а) в его поперечном сечении возникает крутящий момент 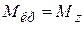 (рис. 4.1).
(рис. 4.1).
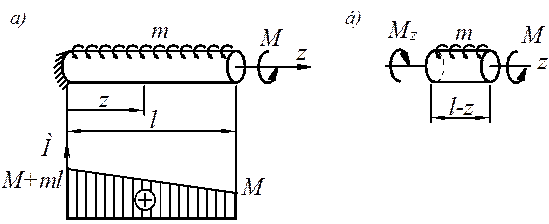
Рис. 4.1
Методом сечений определяем внутренний момент (рис. 4.1 б):
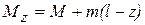 . (4.1)
. (4.1)
Крутящий момент считаем положительным, если он вращает против часовой стрелки, если смотреть на него со стороны внешней нормали к сечению. Соответственно (4.1) позволяет построить график-эпюру изменения 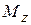 в виде прямой линии при
в виде прямой линии при 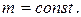
Дифференцируя (4.1), получаем зависимость Журавского
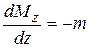 ,
,
связывающую внутренний 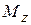 и внешний распределенный момент
и внешний распределенный момент 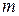 .
.
Из этой зависимости следуют простые правила контроля правильности построения эпюры внутренних крутящих моментов:
1) на незагруженном участке стержня (m = 0), 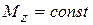 ;
;
2) на равномерно загруженном участке стержня (m = const) момент
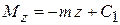 −
−
прямая линия, возрастающая при m < 0 и убывающая при m > 0;
3) в сечении, где действует сосредоточенный момент, в эпюре наблюдается скачок на величину этого момента.
Угол поворота поперечного сечения стержня определяется по формуле
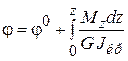 ,
,
где 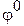 – угол поворота левого торцевого сечения в начале координат,
– угол поворота левого торцевого сечения в начале координат, 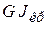 – жесткость при кручении; G – модуль сдвига Кулона;
– жесткость при кручении; G – модуль сдвига Кулона; 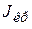 – геометрическая жесткость при кручении стержня.
– геометрическая жесткость при кручении стержня.
Если 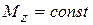 , то
, то
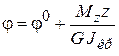 .
.
При 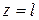 получаем угол поворота правого торцевого сечения относительно левого:
получаем угол поворота правого торцевого сечения относительно левого:
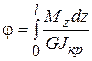 ;
; 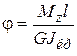 , (
, (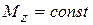 ).
).
На рис. 4.2 изображена эпюра касательных напряжений для различных поперечных сечений. Максимальное напряжение в поперечном сечении и условие прочности имеют вид
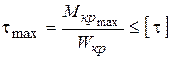 ,
,
где 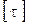 – допускаемое касательное напряжение;
– допускаемое касательное напряжение; 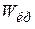 – геометрический момент сопротивления сечения кручению.
– геометрический момент сопротивления сечения кручению.
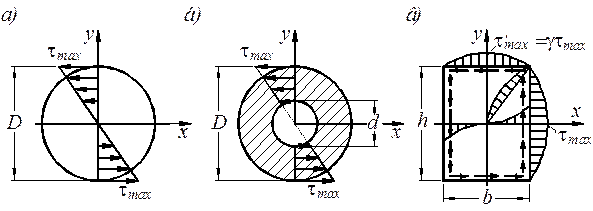
Рис. 4.2
Для круглого поперечного сечения диаметра 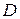 (рис. 4.2 а)
(рис. 4.2 а)
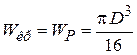 .
.
Для кольцевого сечения (рис. 4.2 б)
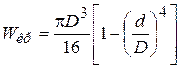 .
.
Для тонкостенной трубки толщиной 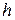 и радиусом
и радиусом 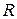
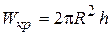 .
.
Для прямоугольного сечения со сторонами 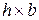 (рис. 4.2 в)
(рис. 4.2 в)
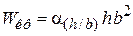 ,
, 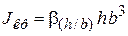 .
.
Момент сопротивления и геометрическая жесткость содержат множители 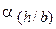 и
и 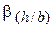 , зависящие от отношения сторон
, зависящие от отношения сторон 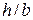 . Значения коэффициентов приведены в таблице:
. Значения коэффициентов приведены в таблице:
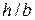
| 1,5 | 1,75 | ∞ | |||||
| α | 0,208 | 0,231 | 0,239 | 0,246 | 0,276 | 0,299 | 0,313 | 1/3 |
| β | 0,141 | 0,196 | 0,214 | 0,229 | 0,263 | 0,299 | 0,313 | 1/3 |
| γ | 0,859 | 0,820 | 0,795 | 0,753 | 0,743 | 0,742 | 0,742 |
Сечения тонкостенных стержней открытого профиля (узкий прямоугольник, двутавр, швеллер, уголок и др.) состоят из прямоугольников, для которых обычно 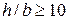 , поэтому для них имеют место расчетные формулы
, поэтому для них имеют место расчетные формулы
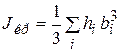 ,
, 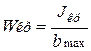 ,
,
где 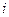 – номер прямоугольной части сечения тонкостенного профиля.
– номер прямоугольной части сечения тонкостенного профиля.
 2015-04-12
2015-04-12 269
269







