1. Уравнения равновесия
Вычисляем сумму всех внешних моментов, действующих на стержень, круглого поперечного сечения и приравниваем ее к нулю
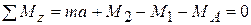 .
.
С учетом 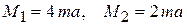 получим реактивный момент в заделке
получим реактивный момент в заделке
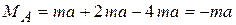 .
.
2. Определение выражений крутящих моментов методом сечений и построение эпюры 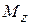
Стержень имеет два участка, на которых выражения крутящих моментов различны. Рассекаем стержень на первом и втором участках и рассматриваем в каждом из этих случаев одну из отсеченных частей (рис. 4.4 б).
| а) в) г) | 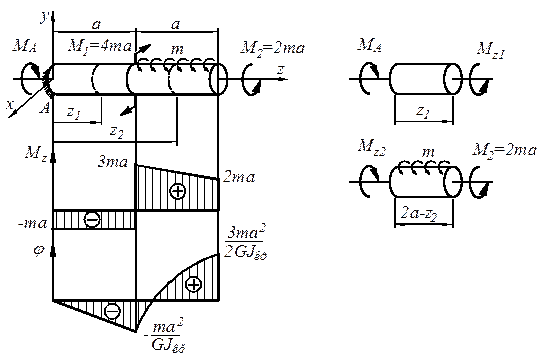
| ||
| Рис. 4.4 |
Для первого участка (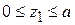 )
)
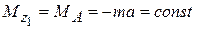 ,
,
для второго (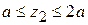 )
)
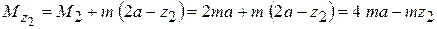 .
.
Строим эпюру крутящих моментов. На первом участке откладываем отрицательное постоянное значение 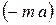 . На втором участке эпюра – прямая линия. Для ее построения достаточно иметь две точки: при
. На втором участке эпюра – прямая линия. Для ее построения достаточно иметь две точки: при 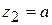 и
и 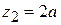 . Соответствующие моменты
. Соответствующие моменты 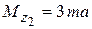 и
и 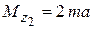 . Наносим на график эти точки и проводим прямую линию (рис. 4.4 в). В сечениях, где действуют сосредоточенные моменты, имеют место скачки, равные по величине значениям этих моментов. Наибольший момент возникает в сечении
. Наносим на график эти точки и проводим прямую линию (рис. 4.4 в). В сечениях, где действуют сосредоточенные моменты, имеют место скачки, равные по величине значениям этих моментов. Наибольший момент возникает в сечении 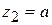 :
:
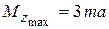 .
.
3. Контроль правильности построенной эпюры с помощью дифференциальной зависимости Д. Журавского
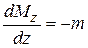 ,
,
позволяющей установить следующие правила:
на незагруженном участке 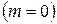 эпюра
эпюра 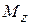 постоянна;
постоянна;
на равномерно загруженном участке 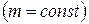 эпюра − прямая линия
эпюра − прямая линия 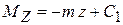 , возрастающая с ростом
, возрастающая с ростом 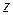 , если
, если 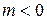 , и убывающая, если
, и убывающая, если 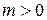 ;
;
в сечениях, где действует сосредоточенный момент, имеет место скачок на величину этого момента.
В нашем примере все правила контроля выполняются.
4. Расчет на прочность при кручении бруса
Условие прочности при кручении
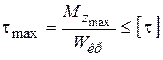 .
.
Так как 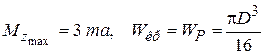 , то получаем
, то получаем
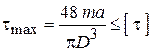 .
.
Если 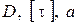 известны, то находим допустимое значение момента
известны, то находим допустимое значение момента
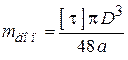 .
.
При проектировочном расчете находим размер поперечного сечения, т.е. диаметр
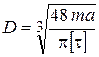 .
.
В этом случае должны быть известны 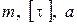 .
.
Третий тип расчета – проверочный.
5. Построение эпюры угловых перемещений 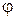 (рис. 4.4 г)
(рис. 4.4 г)
Угловые перемещения находим по формуле
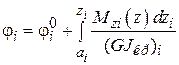 ,
,
где 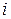 − номер участка,
− номер участка, 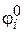 − значение угла в начале
− значение угла в начале 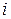 -го участка,
-го участка, 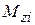 − крутящий момент на
− крутящий момент на 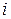 -м участке,
-м участке, 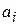 − координата начала
− координата начала 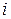 -го участка,
-го участка, 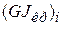 − жесткость при кручении на i -м участке.
− жесткость при кручении на i -м участке.
На первом участке 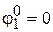 (защемление).
(защемление).
Угол поворота
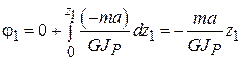 .
.
Эпюра – прямая линия. При 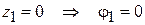 , при
, при 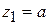 получим
получим 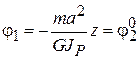 .
.
На втором участке
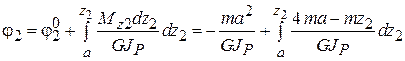 ,
,
или
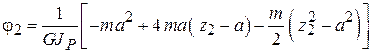 .
.
График-эпюра 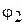 − квадратичная парабола.
− квадратичная парабола.
При 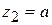 получаем
получаем 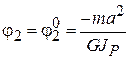 , при
, при 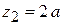 −
− 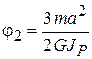 .
.
Выпуклость параболы определяется знаком второй производной. Производные
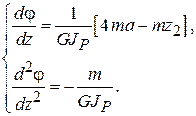
Так как в задаче 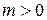 , то
, то 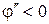 и выпуклость эпюры обращена кверху. Первая производная обращается в нуль при
и выпуклость эпюры обращена кверху. Первая производная обращается в нуль при 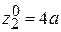 , что за пределами стержня, поэтому эпюра
, что за пределами стержня, поэтому эпюра 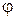 не имеет экстремума.
не имеет экстремума.
Помимо условия прочности иногда проверяется условие жесткости при кручении
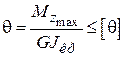 ,
,
где 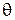 − относительный угол закручивания,
− относительный угол закручивания, 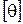 − допускаемое значение относительного угла закручивания.
− допускаемое значение относительного угла закручивания.
№3. Стальной консольный вал (рис. 4.5 а), имеющий участки с разными поперечными сечениями (круглое и прямоугольное), нагружен внешними крутящими моментами. Требуется: из условия прочности определить допускаемую величину крутящих моментов; построить эпюры касательных напряжений для круглого и прямоугольного поперечных сечений;
построить эпюру углов закручивания по длине вала.
Принять 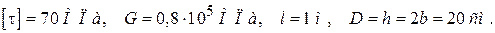
 2015-04-12
2015-04-12 259
259








