2015-04-12
210
1. Определение опорного реактивного момента из уравнения равновесия
Из рис. 4.3 а получаем
,
.
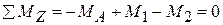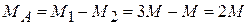2. Определение внутренних крутящих моментов методом сечений
У стержня два участка с различными выражениями для внутреннего крутящего момента. Методом сечения находим (рис. 4.3 б)
, 
,
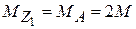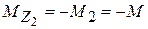и строим эпюру крутящих моментов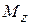 
(рис. 4.3 в).
В сечении на стыке участков действует сосредоточенный момент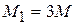 
. В этом сечении на эпюре имеет место скачок на величину этого момента в сторону уменьшения 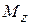. На незагруженных участках стержня, согласно дифференциальной зависимости Д. Журавского, 
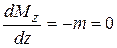, откуда 
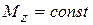, что соответствует построенной эпюре (рис. 4.3 в).
| а) в) г) |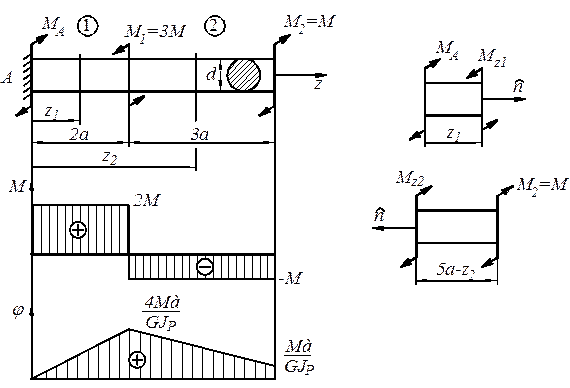 
| ||
| Рис. 4.3 |
3. Расчет на прочность
Из эпюры крутящих моментов определяем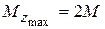 
во всех сечениях первого участка. Условиепрочности
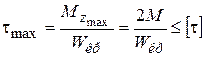. (1)
Если сечение круглое, то
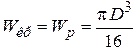, (2)
и тогда из условия прочности (1) получаем
.
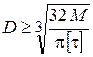Если, например,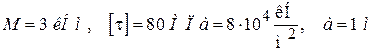 
, то
.
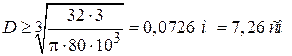Округляем полученные значения до целых значений и принимаем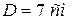 
. Делаем контрольную проверку условия прочности при новом значении диаметра D=7 см. В результате вычислений по формулам (1), (2) получаем
,
.
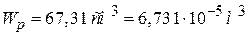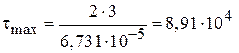
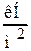
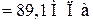Перенапряжение составит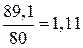 
, т.е. 
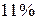. Если принять D=8 см, то 
, 
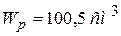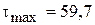
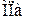, что меньше допускаемого напряжения на 25,4 %. Окончательно принимаем D=8 см.
4. Построение эпюры углов закручивания (рис. 4.3 г)
На первом участке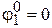 
, поэтому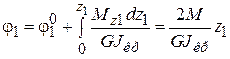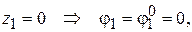
.
При 
а при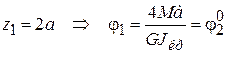 
.
На втором участке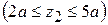 
имеем
.
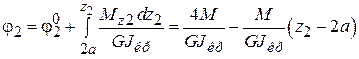При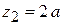 
получаем 
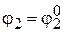, а при 
.
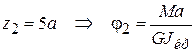№2. Построить эпюры крутящих моментов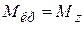 
и угловых перемещений 
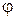, произвести расчеты на прочность и жесткость (рис. 4.4).
