Векторное произведение векторов 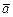 и
и 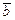 - вектор
- вектор 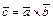 , определяемый условиями:
, определяемый условиями:
1) 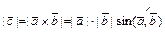 ; 2)
; 2) 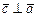 и
и 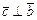 ; 3)
; 3) 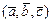 - правая тройка векторов.
- правая тройка векторов.
Векторное произведение обладает свойствами:
1) 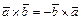 ; 2)
; 2) 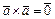 3)
3) 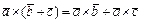 ; 4)
; 4) 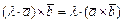 , где
, где 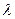 - число;
- число;
Для векторов канонического базиса 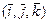 :
: 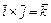 ,
, 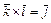 ,
, 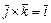 ,
, 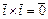 ,
, 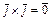 ,
, 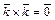 .
.
Для векторов 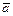 и
и 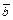 , заданных координатами
, заданных координатами 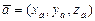 ,
, 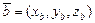 :
: 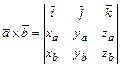
Некоторые приложения векторного произведения:
1) Вычисление площадей треугольника и параллелограмма: 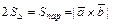 .
.
2) Установление параллельности векторов 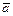 и
и 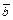 :
: 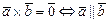 .
.
 2015-04-12
2015-04-12 308
308








