ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Задача 1
Варианты 1- 35. Докажите равенство двух множеств E и F.
Вариант 1. 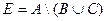 ,
, 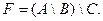 .
.
Вариант 2. 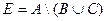 ,
, 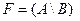
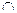
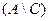 .
.
Вариант 3. 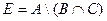 ,
, 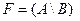
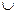
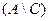 .
.
Вариант 4. 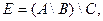
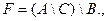
Вариант 5. 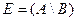
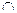 B,
B, 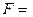 Æ.
Æ.
Вариант 6. 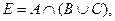
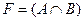
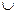
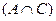 .
.
Вариант 7. 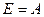 ,
, 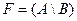
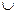
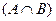 .
.
Вариант 8. 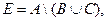
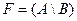
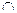
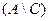 .
.
Вариант 9. 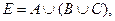
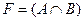
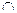
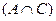 .
.
Вариант 10. 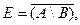
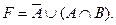
Вариант 11. 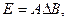
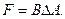
Вариант 12. 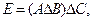
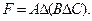
Вариант 13. 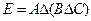
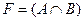
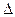
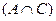
Вариант 14. 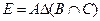 ,
, 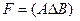
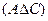 .
.
Вариант 15. 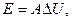
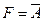 .
.
Вариант 16. 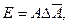
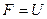 .
.
Вариант 17. 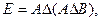
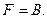
Вариант 18. 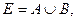
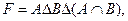
Вариант 19. 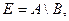
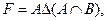
Вариант 20. 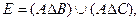
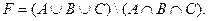
Вариант 21. 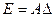 Æ,
Æ, 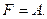
Вариант 22. 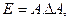
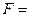 Æ.
Æ.
Вариант 23. 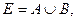
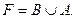
Вариант 24. 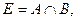
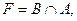
Вариант 25. 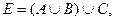
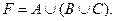
Вариант 26. 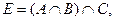
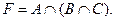
Вариант 27. 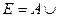 Æ,
Æ, 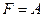 .
.
Вариант 28. 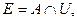
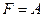 .
.
Вариант 29. 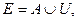
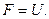
Вариант 30. 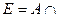 Æ,
Æ, 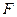 =Æ.
=Æ.
Вариант 31. 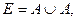
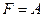 .
.
Вариант 32. 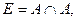
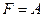 .
.
Вариант 33. 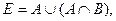
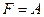 .
.
Вариант 34. 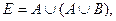
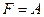 .
.
Вариант 35. 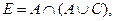
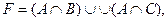
Вариант 36. 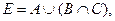
РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Вариант 28. Докажите равенство двух множеств E и F, где
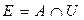 ,
, 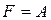 .
.
Доказательство. Пусть А – произвольное множество, U – универсальное множество. Необходимо доказать следующее свойство для операции пересечения множеств:
А 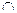 U = A.
U = A.
Известно, что
1) E 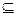 F;
F;
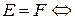 2) F
2) F 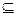 E.
E.
В свою очередь:
1) E 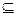 F
F 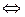 (
(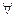
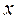
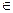 E) [
E) [ 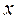
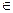 F ];
F ];
2) F 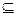 E
E 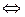 (
(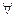
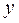
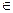 F) [
F) [ 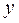
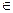 E ].
E ].
Поэтому докажем, что каждое множество, стоящее по одну сторону от знака равенства, включено во множество, стоящее по другую сторону от этого знака равенства.
1) По определению пересечения
А 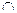 U
U 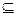 А. (1)
А. (1)
2) Если у – произвольный элемент из множества А, то также у 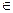 U, так как А
U, так как А 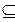 U. Поэтому согласно определению пересечения
U. Поэтому согласно определению пересечения 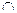 элемент у
элемент у 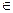 А
А 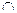 U. Имеем
U. Имеем
(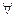 у
у 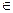 А) [ у
А) [ у 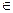 A
A 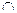 U ],
U ],
что означает
А 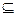 А
А 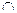 U. (2)
U. (2)
Из условий (1) и (2) следует равенство А 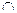 U = A.
U = A.
Что и требовалось доказать.
Вариант 6. Докажите равенство двух множеств E и F.
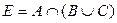 ,
, 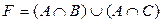 .
.
Решение. 1) Пусть 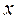 – произвольный элемент из множества
– произвольный элемент из множества 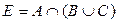 . По определению операции пересечения
. По определению операции пересечения 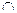 :
: 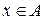 и
и 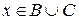 . Условие
. Условие 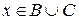 означает, что
означает, что 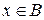 или
или 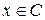 . Итак, имеем
. Итак, имеем 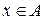 ,
, 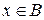 или
или 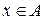 ,
, 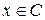 .
.
a) Предположим, что 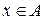 ,
, 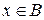 . Тогда
. Тогда 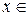 A
A 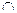 B. По определению объединения
B. По определению объединения 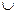 :
: 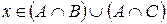 , так как этот элемент принадлежит хотя бы одному из составляющих
, так как этот элемент принадлежит хотя бы одному из составляющих 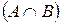 или
или 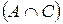 . В случае а) из условия
. В случае а) из условия 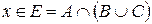 вытекает, что
вытекает, что 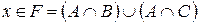 .
.
б) Пусть теперь 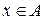 ,
, 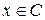 . Тогда
. Тогда 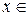 A
A 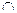 С, а по определению пересечения
С, а по определению пересечения 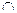 :
: 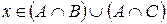 . Видим что и в случае б) из условия
. Видим что и в случае б) из условия 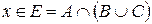 вытекает, что
вытекает, что 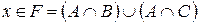 .
.
Итак, в случае 1):
E 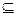 F. (*).
F. (*).
2). Обратно, возьмём любой элемент 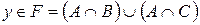 . По определению объединения
. По определению объединения 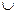 :
: 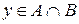 или
или 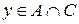 .
.
a) Пусть 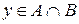 . Тогда по определению пересечения
. Тогда по определению пересечения 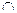 :
: 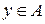 ,
, 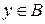 .
.
Поскольку 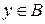 , то
, то 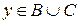 . Имеем
. Имеем 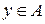 ,
, 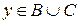 . По определению пересечения
. По определению пересечения 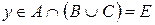 . В случае а) из условия
. В случае а) из условия 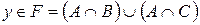 следует, что
следует, что 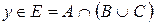 .
.
б) Пусть 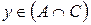 , т.е.
, т.е. 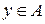 ,
, 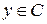 . Тогда
. Тогда 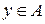 ,
, 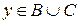 и по определению пересечения
и по определению пересечения 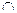 :
: 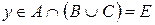 . Опять видим, что из условия
. Опять видим, что из условия 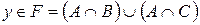 вытекает
вытекает 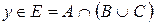 . Итак, в случае 2)
. Итак, в случае 2)
F 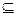 E. (**).
E. (**).
Из (*) и (**) получаем 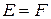 .
.
Что и требовалось доказать.
 2015-04-12
2015-04-12 1317
1317







